
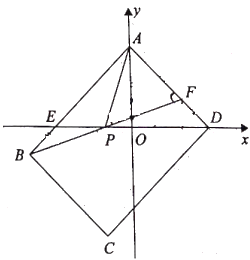
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在坐标轴上,两点的坐标分别是点
在坐标轴上,两点的坐标分别是点![]() 点
点![]() 且
且![]() 满足:
满足:![]()
![]() 边
边![]() 与
与![]() 轴交于点
轴交于点![]() 点
点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,分别与
,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 点
点![]() 且
且![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 求证:
求证:![]() ;
;
(3)若点![]() 的纵坐标为
的纵坐标为![]() 则线段HF的长为 .(用含
则线段HF的长为 .(用含![]() 的代数式表示)
的代数式表示)
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)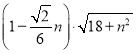 .
.
【解析】
(1)根据二次根式有意义被开方数非负和算术平方根的非负性列出两个不等式,求公共解即可求出m的值;
(2)作![]() 轴,
轴,![]() 轴,证明
轴,证明![]() 可得BP=PF,再根据直角三角形斜边上的中线等于斜边的一半可得
可得BP=PF,再根据直角三角形斜边上的中线等于斜边的一半可得![]() ,然后结合等腰三角形的性质,利用三角形的内角和定理分别求出
,然后结合等腰三角形的性质,利用三角形的内角和定理分别求出![]() 和
和![]() ,可得它们相等;
,可得它们相等;
(3)分别表示AF和AB,利用勾股定理求得BF的长,即可求得PF的长,再表示ON和PN的长度,利用平行线分线段成比例即可求得HF.
(1)∵![]()
![]() ,
,
∴![]() ,且
,且 ![]() ,
,
![]() ;
;
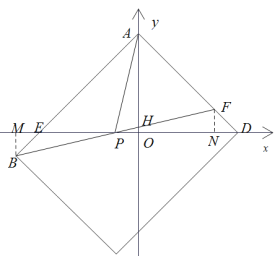
![]() 作
作![]() 轴,
轴,![]() 轴
轴
![]() ,
,
![]() ,
,
∵四边形![]() 为矩形,
为矩形,
∴∠EAD=90°,
∴![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
∵![]() 轴,
轴,![]() 轴
轴
![]() ,
,
在![]() 和
和![]() 中
中
∵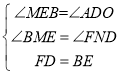 ,
,
∴![]() ≌
≌![]() ,
,
![]() ,
,
在![]() 和
和![]() 中,
中,
∵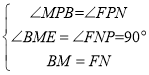
∴![]() ,
,
![]() ,
,![]() ,
,
∵![]() 中,
中,![]() ,
,
![]()
![]() ,
,![]() ,
,
∴![]() ;
;
(3)∵F点的纵坐标为n,
由(2)可知FN=ND=ME=BM=n,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
在Rt△ABF中,根据勾股定理、
![]() ,
,
∴![]() ,
,
∵FN⊥x轴,
∴FN∥OH,
∴![]() ,即
,即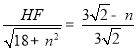 ,
,
解得:![]() ,
,
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在某地,人们发现在一定温度下某种蟋蟀叫的次数与温度之间有如下的竟是关系:

(1)在这个变化过程中,自变量是 ,因变量是 ;
(2)在当地温度![]() 每增加
每增加![]() ,这种蟋蟀
,这种蟋蟀![]() 叫的次数
叫的次数![]() 是怎样变化的?
是怎样变化的?
(3)这种蟋蟀![]() 叫的次数
叫的次数![]() (次)与当地温度
(次)与当地温度![]() 之间的关系为 ;
之间的关系为 ;
(4)当这种蟋蟀![]() 叫的次数
叫的次数![]() 时,求当时该地的温度.
时,求当时该地的温度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某商场为了吸引顾客,开展有奖促销活动,设立了一个可以自由转动的转盘,转盘被分成4个面积相等的扇形,四个扇形区域里分别标有“10元”、“20元”、“30元”、“40元”的字样(如图).规定:同一日内,顾客在本商场每消费满100元就可以转动转盘一次,商场根据转盘指针指向区域所标金额返还相应数额的购物券,某顾客当天消费240元,转了两次转盘.

(1)该顾客最少可得_________元购物券,最多可得_________元购物券;
(2)请用画树状图或列表的方法,求该顾客所获购物券金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
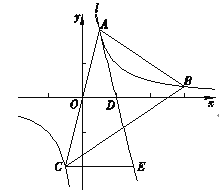
查看答案和解析>>
科目:初中数学 来源: 题型:
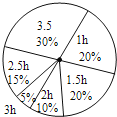
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分14分)在平面直角坐标系内,已知点A(0,6)、点B(8,0),动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O移动,同时动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A移动,设点P、Q移动的时间为t秒.
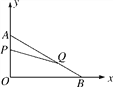
(1)求直线AB的解析式;
(2)当t为何值时,以点A、P、Q为顶点的三角形与△AOB相似?
(3)当t=2秒时,四边形OPQB的面积为多少个平方单位?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm![]() ?
?
(2)△PAQ的面积能否达到3 cm![]() ?
?
(3)经过多长时间,P、Q两点之间的距离为![]() cm?
cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).

(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com