
【题目】如图所示:在平面直角坐标系中,四边形OACB为矩形,C点坐标为(3,6),若点P从O点沿OA向A点以1cm/s的速度运动,点Q从A点沿AC以2cm/s的速度运动,如果P、Q分别从O、A同时出发,问:
(1)经过多长时间△PAQ的面积为2cm![]() ?
?
(2)△PAQ的面积能否达到3 cm![]() ?
?
(3)经过多长时间,P、Q两点之间的距离为![]() cm?
cm?

科目:初中数学 来源: 题型:
【题目】一个硬币抛起后落地时“正面朝上”的概率有多大?
(1)写出你的猜测;
(2)一位同学在做这个试验时说:“我只做了10次试验就得到了正面朝上的概率约为30%.”你认为他说的对吗?为什么?
(3)还有一位同学在做这个试验中觉得用硬币麻烦,改用可乐瓶盖做这个试验,你认为他的做法科学吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中, ![]() =8
=8![]() ,
, ![]() =6
=6![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 以2
以2 ![]() 的速度向终点
的速度向终点![]() 匀速运动,同时点
匀速运动,同时点![]() 从点
从点![]() 出发,沿
出发,沿![]() →
→![]() 以4
以4 ![]() 的速度向点
的速度向点![]() 匀速运动,到达点
匀速运动,到达点![]() 后,继续沿
后,继续沿![]() →
→![]() 以3
以3 ![]() 的速度向终点
的速度向终点![]() 匀速运动.连结
匀速运动.连结![]() ,以
,以![]() 、
、![]() 为边作□
为边作□![]() ,连结
,连结![]() 交
交![]() 于点
于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (
(![]() ),□
),□![]() 与矩形
与矩形![]() 重叠部分图形的面积为
重叠部分图形的面积为![]() .
.
(1)当点![]() 在点
在点![]() 上,△
上,△![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
(2)当点![]() 在边
在边![]() 上,△
上,△![]() 与△
与△![]() 相似时,求
相似时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
(4)当△![]() 是等腰三角形时,直接写出
是等腰三角形时,直接写出![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
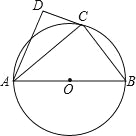
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。

其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC内接于⊙O,过点A作直线EF.

(1)如图①所示,若AB为⊙O的直径,要使EF成为⊙O的切线,还需要添加的一个条件是(至少说出两种): 或者 .
(2)如图②所示,如果AB是不过圆心O的弦,且∠CAE=∠B,那么EF是⊙O的切线吗?试证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各项是真命题的是( )
A. 从直线外一点到已知直线的垂线段叫做这点到直线的距离
B. 过一点有且只有一条直线与已知直线垂直
C. 有公共顶点且相等的两个角是对顶角
D. 同一平面内,两条直线的位置关系只有相交和平行两种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小李在一次高尔夫球选拔赛中,从山坡下O点打出一球向球洞A点飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大水平高度12米时,球移动的水平距离为9米.已知山坡OA与水平方向OC的夹角为30o,O、A两点相距8![]() 米.
米.

(1)求直线OA的解析式;
(2)求出球的飞行路线所在抛物线的解析式;
(3)判断小李这一杆能否把高尔夫球从O点直接打入球洞A点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com