
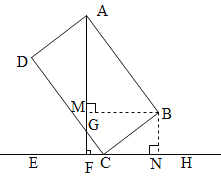
【题目】如图①是一个新款水杯,水杯不盛水时按如图②所示的位置放置,这样可以快速晾干杯底,干净透气;将图②的主体部分抽象成图③,此时杯口与水平直线的夹角为37°,四边形ABCD可以看作矩形,测得AB=10cm,BC=8cm,过点A作AF⊥CE,交CE于点F.
(1)求∠BAF的度数;
(2)求点A到水平直线CE的距离AF的长 (参考数据sin37°≈0.6,cos37°≈0.8,tan37°≈0.75).

【答案】(1)37°;(2)12.8cm.
【解析】试题分析:(1)由矩形的性质得到∠BCD=90°,DC∥AB,再由平行线的性质得到∠BAF=∠CGF,由余角的性质得到∠CGF=∠BCH,即可得出结果;
(2)作BM⊥AF于M,BN⊥EF于N,由三角函数得出MF,AM的长,即可得出结果.
试题解析:解:(1)如图,∵四边形ABCD是矩形,∴∠BCD=90°,DC∥AB,∴∠BAF=∠CGF,∴∠BCH+∠GCE=90°,∵∠CGF+∠GCE=90°,∴∠CGF=∠BCH=37°,∴∠BAF=∠CGF=37°.

(2)如图,过点B作BM⊥AF于M,BN⊥EF于N,则MF=BN=BC·sin37°≈8×0.6≈4.8(cm),AM=AB·cos37°≈10×0.8≈8(cm),∴AF=AM+MF≈8+4.8≈12.8(cm),即点A到水平直线CE的距离AF的长约为12.8cm.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在“端午”期间,小明、小亮等同学随家长一同到某公园游玩,下面是购买门票时,小明与他爸爸的对话(如图),试根据图中的信息,解答下列问题:
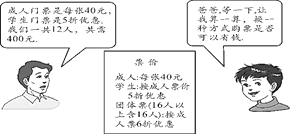
(1)他们共去了几个成人,几个学生?
(2)请你帮助算算,小明用更省钱的购票方式是指什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 (本小题8分)已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.

(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是坐标原点,直线OA与双曲线![]() 在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=
在第一象限内交于点A,过点A作AB⊥x轴,垂足为B,若OB=4,tan∠AOB=![]() .
.
(1)求双曲线的解析式;
(2)直线AC与y轴交于点C(0,1),与x轴交于点D,求D点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=![]() 时,求CG的长;
时,求CG的长;
(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在坐标轴上,两点的坐标分别是点
在坐标轴上,两点的坐标分别是点![]() 点
点![]() 且
且![]() 满足:
满足:![]()
![]() 边
边![]() 与
与![]() 轴交于点
轴交于点![]() 点
点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,分别与
,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 点
点![]() 且
且![]() .
.
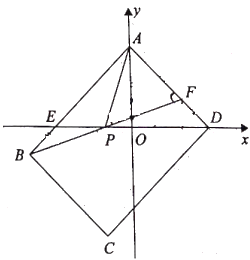
(1)求![]() 的值;
的值;
(2)若![]() 求证:
求证:![]() ;
;
(3)若点![]() 的纵坐标为
的纵坐标为![]() 则线段HF的长为 .(用含
则线段HF的长为 .(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com