
【题目】已知:如图,二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).

(1)写出该函数图象的对称轴;
(2)若将线段OA绕点O逆时针旋转60°到OA′,试判断点A′是否为该函数图象的顶点?请说明理由.
【答案】(1)直线x=1 (2)点A′为抛物线y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点
的顶点
【解析】
试题分析:(1)把已知点O、A代入函数的解析式可求出h的值h=1,及a=![]() ,然后根据二次函数的顶点式的特点判断出对称轴;
,然后根据二次函数的顶点式的特点判断出对称轴;
(2)由线段OA绕点O逆时针旋转60°到OA′,可知OA′=OA=2,∠A′OA=60°,如图,作A′B⊥x轴于点B,根据直角三角形的特点可知sin60°=![]() ,cos60°=
,cos60°=![]() ,因此可求得A′B=OA′sin60°=
,因此可求得A′B=OA′sin60°=![]() =
=![]() ,OB=OA′cos60°=
,OB=OA′cos60°=![]() =1,所以A′点的坐标为(1,
=1,所以A′点的坐标为(1,![]() ),点A′正好是二次函数y=﹣
),点A′正好是二次函数y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点.
的顶点.
试题解析:解:(1)∵二次函数y=a(x﹣h)2+![]() 的图象经过原点O(0,0),A(2,0).
的图象经过原点O(0,0),A(2,0).
∴抛物线的对称轴为直线x=1;
点A′是该函数图象的顶点.理由如下:

如图,作A′B⊥x轴于点B
∵线段OA绕点O逆时针旋转60°到OA′,
∴OA′=OA=2,∠A′OA=60°,
在Rt△A′OB中,
A′B=OA′sin60°=![]() =
=![]() ,
,
∴OB=OA′cos60°=![]() =1.
=1.
∴A′点的坐标为(1,![]() ),
),
∴点A′为抛物线y=﹣![]() (x﹣1)2+
(x﹣1)2+![]() 的顶点.
的顶点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的顶点
的顶点![]() 在坐标轴上,两点的坐标分别是点
在坐标轴上,两点的坐标分别是点![]() 点
点![]() 且
且![]() 满足:
满足:![]()
![]() 边
边![]() 与
与![]() 轴交于点
轴交于点![]() 点
点![]() 是边
是边![]() 上一动点,连接
上一动点,连接![]() ,分别与
,分别与![]() 轴,
轴,![]() 轴交于点
轴交于点![]() 点
点![]() 且
且![]() .
.
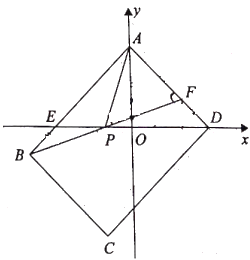
(1)求![]() 的值;
的值;
(2)若![]() 求证:
求证:![]() ;
;
(3)若点![]() 的纵坐标为
的纵坐标为![]() 则线段HF的长为 .(用含
则线段HF的长为 .(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县举办老、中、青三个年龄段五公里竞走活动,其人数比为![]() ,如图所示的扇形统计图表示 上述分布情况,已知老人有
,如图所示的扇形统计图表示 上述分布情况,已知老人有![]() 人,则下列说法不正确的是( )
人,则下列说法不正确的是( )
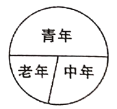
A. 老年所占区域的圆心角是![]() B. 参加活动的总人数是
B. 参加活动的总人数是![]() 人
人
C. 中年人比老年人多![]() D. 老年人比青年人少
D. 老年人比青年人少![]() 人
人
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:抛物线![]() .
.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果二次函数的二次项系数为1,那么此二次函数可表示为y=x2+px+q,我们称[p,q]为此函数的特征数,如函数y=x2+2x+3的特征数是[2,3].
(1)若一个函数的特征数为[-2,1],求此函数图象的顶点坐标;
(2)探究下列问题:
①若一个函数的特征数为[4,-1],将此函数的图象先向右平移1个单位长度,再向上平移1个单位长度,求得到的图象对应的函数的特征数;
②若一个函数的特征数为[2,3],问此函数的图象经过怎样的平移,才能使得到的图象对应的函数的特征数为[3,4]?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=(m-1)x2+m2-2m-2的图象开口向下,且经过点(0,1).
(1)求m的值;
(2)求此抛物线的顶点坐标及对称轴;
(3)当x为何值时,y随x的增大而增大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市居民用电的电价实行阶梯收费,收费标准如下表:
一户居民每月用电量x(单位:度) | 电费价格(单位:元/度) |
0<x≤200 | a |
200<x≤400 | b |
x>400 | 0.92 |
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系,直线y=2x+2交x轴于A,交y轴于 D,

(1)直接写直线y=2x+2与坐标轴所围成的图形的面积
(2)以AD为边作正方形ABCD,连接AD,P是线段BD上(不与B,D重合)的一点,在BD上截取PG=![]() ,过G作GF垂直BD,交BC于F,连接AP.
,过G作GF垂直BD,交BC于F,连接AP.
问:AP与PF有怎样的数量关系和位置关系?并说明理由;
(3)在(2)中的正方形中,若∠PAG=45°,试判断线段PD,PG,BG之间有何关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com