
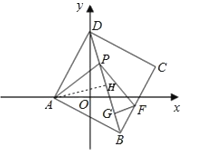
����Ŀ����ƽ��ֱ������ϵ��ֱ��y=2x+2��x����A����y���� D��

��1��ֱ��дֱ��y=2x+2����������Χ�ɵ�ͼ�ε����
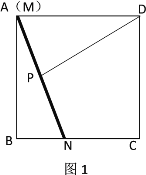
��2����ADΪ����������ABCD������AD��P���߶�BD�ϣ�����B��D�غϣ���һ�㣬��BD�Ͻ�ȡPG=![]() ����G��GF��ֱBD����BC��F������AP��
����G��GF��ֱBD����BC��F������AP��
�ʣ�AP��PF��������������ϵ��λ�ù�ϵ����˵�����ɣ�
��3���ڣ�2���е��������У�����PAG=45�������ж��߶�PD��PG��BG֮���кι�ϵ����˵�����ɣ�
���𰸡���1��1����2��AP=PF��AP��PF�����ɼ���������3��PD2+BG2=PG2�����ɼ�����
��������
��1���ȸ���һ�κ�������ʽ���A,D�����꣬���������ε������ʽ������⣻
��2������A��AH��DB���ȼ����AD=![]() �����������ε����ʵõ�BD=
�����������ε����ʵõ�BD=![]() ��AH=DH=
��AH=DH=![]() BD=
BD=![]() ����PG=
����PG=![]() ���õ�DP+BG=
���õ�DP+BG=![]() ����PH=BG,��֤��Rt��APH��Rt��PFG�����ɵõ�AP=PF��AP��PF��
����PH=BG,��֤��Rt��APH��Rt��PFG�����ɵõ�AP=PF��AP��PF��
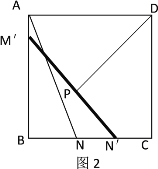
��3������AGB�Ƶ�A����ʱ����ת90���õ���AMD���ɵá�MDA=��ABG=45����DM=BG, ��MAD=��BAG,AM=AG,���MDP=90�������ݹ��ɶ�����DP2+BG2=PM2,�ɡ�PAG=45�����ɵá�DAP+��BAG=45��������MAP=45������֤�á�AMP�ա�AGP���õ�MP=PG,����DP2+BG2=PM2��
��1����ֱ��y=2x+2��x����A����y���� D��
��x=0�����y=2����D��0��2��
��y=0�����x=-1����A��-1��0��
��AO=1��DO=2��
��ֱ��y=2x+2����������Χ�ɵ�ͼ�Ρ�AOD=![]() ��1��2=1��
��1��2=1��
��2��AP=PF��AP��PF���������£�
����A��AH��DB����ͼ��
��A��-1��0����D��0��2��
��AD=![]() =
=![]() =AB��
=AB��
���ı���ABCD��������
��BD=![]() =
=![]() ��
��
��AH=DH=![]() BD=
BD=![]() ��
��
��PG=![]() ��
��
��DP+BG=![]() ��
��
��DH=DP+PH=![]()
��PH=BG,
�ߡ�GBF=45��
��BG=GF=HP
��Rt��APH��Rt��PFG��
��AP=PF, ��PAH=��PFG
���APH+��GPF=90����AP��PF��
��3��PD2+BG2=PG2���������£�
��ͼ������AGB�Ƶ�A����ʱ����ת90���õ���AMD������MP��
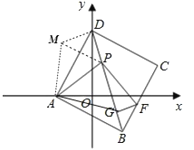
���MDA=��ABG=45����DM=BG, ��MAD=��BAG,AM=AG,
���MDP=90����
��DP2+BG2=PM2,
�֡ߡ�PAG=45����
���DAP+��BAG=45����
���MAD+��DAP =45��������MAP=45����
��AM=AG��
���AMP�ա�AGP��
��MP=PG,
��PD2+BG2=PG2


 �ο�������ϵ�д�
�ο�������ϵ�д� ������ѧ��ʱ��ҵϵ�д�
������ѧ��ʱ��ҵϵ�д� ���������ʱ��ѵϵ�д�
���������ʱ��ѵϵ�д� �㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
�㽭�¿γ���άĿ�������ʱ��ѵϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪:��ͼ�����κ���y=a��x��h��2+![]() ��ͼ��ԭ��O��0��0����A��2��0����
��ͼ��ԭ��O��0��0����A��2��0����

��1��д���ú���ͼ��ĶԳ��
��2�������߶�OA�Ƶ�O��ʱ����ת60�㵽OA�䣬���жϵ�A���Ƿ�Ϊ�ú���ͼ��Ķ��㣿��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��ͼ���һ���֣��Գ�����ֱ��x=1��
��b2��4ac�� ��4a-2b+c��0�� �۲���ʽax2+bx+c��0�Ľ⼯��x��3.5�� ������-2��y1������5��y2�����������ϵ����㣬��y1��y2��
����4���ж��У���ȷ���ǣ�������

A. �٢� B. �٢� C. �٢ۢ� D. �ڢۢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0��������������y=![]() x��ͼ����ͼ��ʾ����ax2+��b��
x��ͼ����ͼ��ʾ����ax2+��b��![]() ��x+c=0��a��0��������֮���� ��
��x+c=0��a��0��������֮���� ��

A. ����0 B. ����0 C. С��0 D. ����ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һ������ʮ�ĵ�������Ϸ������Ϸ�����������ģ���ȡ�ĸ�1��13֮�����Ȼ���������ĸ�����ÿ��������ֻ����һ�Σ����мӼ��˳��������㣬ʹ��������24.�����1��2��3��4�������������㣺(1+2+3)��4��24������������4��(1��2��3)��Ϊ��ͬ���������㣩�����ĸ�������3��4����6��10��������������д�����ֲ�ͬ����������ʽ������ʹ�����ţ�ʹ��������24.����ʽ���£�
��1��____________________________��
��2��____________________________��
��3��____________________________��
�����ĸ�������3����5��7����13����ͨ������ʽ
��4��____________________________ʹ��������24.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x+m��������y=x2+bx+c��������A(1,0)��B(3,2).
(1)��m��ֵ�������ߵĽ���ʽ��
(2)��ʽx2+bx+c>x+m�Ľ⼯(ֱ��д����)��
(3)��M(a,y1),N(a+1,y2)���㶼��������y=x2+bx+c�ϣ��ԱȽ�y1��y2�Ĵ�С.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ͬѧ��ÿ���㻨Ǯ�����УС������������˱�У����ͬѧ�����ݵ������������������в�������ͳ��ͼ��:
������ͳ�Ʊ�

������Ƶ���ֲ�ֱ��ͼ ����������ͳ��ͼ
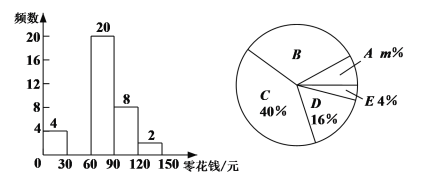
���������ͼ��������������⣺
��1����գ���ε�������������� ��![]() ,
,![]() ��
��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3��������ͳ��ͼ������![]() ��Բ�ĽǶ�����
��Բ�ĽǶ�����
��4����У����![]() �ˣ������ÿ���㻨Ǯ������
�ˣ������ÿ���㻨Ǯ������![]() ��
��![]() ��������.
��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ���̶����ȵ�ľ��![]() ��������
��������![]() ���ڲ���ͼ1���ã���ʱľ���Ķ˵�
���ڲ���ͼ1���ã���ʱľ���Ķ˵�![]() ǡ�����
ǡ�����![]() �غϣ���
�غϣ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ����ľ����
����ľ����![]() ���»���
���»���![]() ����λ������ͼ2��λ�ã�ͬʱ��һ���˵�
����λ������ͼ2��λ�ã�ͬʱ��һ���˵�![]() ��
��![]() ���һ���
���һ���![]() ����λ������
���������![]() ����
����![]() ��
��![]() ���ڻ����Ĺ����У���
���ڻ����Ĺ����У���![]() ��ľ���е�
��ľ���е�![]() ����̾���Ϊ__________��
����̾���Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���P������Ϊ��a��b������P������������P�������궨�����£���![]() ʱ��P��������Ϊ��b��a������
ʱ��P��������Ϊ��b��a������![]() ʱ��P��������Ϊ����a����b����
ʱ��P��������Ϊ����a����b����
��1��д��A��5��3���ı任������_____��B��1��6���ı任������______��C����2��4���ı任������_____��
��2�����ֱ��l��![]() �����е�Ĺ��������һ���µ�ͼ�Σ�����ͼ��W���뻭��ͼ��W��
�����е�Ĺ��������һ���µ�ͼ�Σ�����ͼ��W���뻭��ͼ��W��
��3���ڣ�2���������£���ֱ��y=kx��1��k��0����ͼ��W���������㣬��ֱ��д��k��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com