
【题目】如图,四边形![]() 内接于⊙
内接于⊙![]() ,且
,且![]() .延长
.延长![]() 至点
至点![]() ,使
,使![]() ,连接
,连接![]() .
.
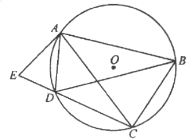
(1)求证:![]() 平分
平分![]() ;
;
(2)若![]() ,求证:
,求证:![]() 是⊙
是⊙![]() 的切线.
的切线.
【答案】(1)见解析;(2)见解析
【解析】
(1)根据同弧所对圆周角相等可得∠ABD=∠ACD,由此可证△ABD≌△ACE,进而可得AD=AE,∠ADB=∠AEC,再由AD=AE得∠ADE=∠AEC,等量代换即可得证;
(2)由AB∥CD得∠ADE=∠BAD,结合∠ADE=∠ADB可得∠ADB=∠BAD,由此可得AB=BD,结合BD=CE,进而可证四边形ABCE为平行四边形,进而得BC∥AE,连接OA、OB、OC,再根据AB=AC,OB=OC可证AO⊥BC,结合BC∥AE即可得证.
(1)证明:由图可知:∠ABD=∠ACD,
∵在△ABD与△ACE中,
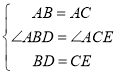
∴△ABD≌△ACE(SAS),
∴AD=AE,∠ADB=∠AEC,
∵AD=AE,
∴∠ADE=∠AEC,
∴∠ADE=∠ADB,
∴AD平分∠BDE;
(2)∵AB∥CD,
∴∠ADE=∠BAD,
∵∠ADE=∠ADB,
∴∠ADB=∠BAD,
∴AB=BD,
∵BD=CE,
∴AB=CE,
∵AB=CE,AB∥CD,
∴四边形ABCE为平行四边形,
∴BC∥AE,
如图,连接OA、OB、OC,
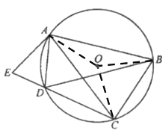
∵AB=AC,OB=OC
∴AO⊥BC,
又∵BC∥AE
∴AO⊥AE,
∴AE是⊙O的切线.


科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华诗词,寓意深广.为了传承优秀传统文化,我市某校团委组织了一次全校2000名学生参加的“中国诗词大会”海选比赛,赛后发现所有参赛学生的成绩均不低于50分,为了更好地了解本次海选比赛的成绩分布情况,随机抽取了其中200名学生的海选比赛成绩(成绩x取整数,总分100分)作为样本进行整理,得到下列统计图表:
抽取的200名学生海选成绩分组表
组别 | 海选成绩x |
A组 | 50≤x<60 |
B组 | 60≤x<70 |
C组 | 70≤x<80 |
D组 | 80≤x<90 |
E组 | 90≤x<100 |
请根据所给信息,解答下列问题:
(1)请把图1中的条形统计图补充完整;(温馨提示:请画在答题卷相对应的图上)
(2)在图2的扇形统计图中,记表示B组人数所占的百分比为a%,则a的值为 ,表示C组扇形的圆心角θ的度数为 度;
(3)规定海选成绩在90分以上(包括90分)记为“优等”,请估计该校参加这次海选比赛的2000名学生中成绩“优等”的有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与坐标轴交于
与坐标轴交于![]() .
.
(1)求抛物线的解析式;
(2)设直线![]() 与该抛物线交于点
与该抛物线交于点![]() (
(![]() 在
在![]() 的左侧),记抛物线在直线
的左侧),记抛物线在直线![]() 下方的图象为
下方的图象为![]() ,在直线
,在直线![]() 下方的图象为
下方的图象为![]() ,将图象
,将图象![]() 沿直线
沿直线![]() 向下翻折得到图象
向下翻折得到图象![]() ,图象
,图象![]() 和图象
和图象![]() 两部分组成的图象记为
两部分组成的图象记为![]() .
.
①设图象![]() 的顶点为
的顶点为![]() ,当
,当![]() 落在
落在![]() 的边上时,求实数
的边上时,求实数![]() 的值.
的值.
②当![]() 时,设
时,设![]() 是图象
是图象![]() 上的动点.
上的动点.
(i)连结![]() ,过线段
,过线段![]() 的中点作
的中点作![]() 轴的平行线交
轴的平行线交![]() 轴于点
轴于点![]() ,当
,当![]() 是以
是以![]() 为直角顶点的直角角形时,直接写出
为直角顶点的直角角形时,直接写出![]() 的值.
的值.
(ii)当![]() 时,
时,![]() 的最小值为
的最小值为![]() ,直接写出
,直接写出![]() 的最大值及相应的
的最大值及相应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的对角线交于点O,以OD,CD为邻边作平行四边形DOEC,OE交BC于点F,连结BE.
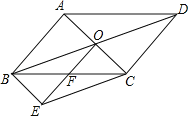
(1)求证:F为BC中点.
(2)若OB⊥AC,OF=1,求平行四边形ABCD的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们学习了勾股定理后,都知道“勾三、股四、弦五”.
观察:3、4、5;5、12、13;7、24、25;9、40、41;…,发现这些勾股数的勾都是奇数,且从3起就没有间断过.
(1)请你根据上述的规律写出下一组勾股数:________.
(2)若第一个数用字母n(n为奇数,且n≥3)表示,那么后两个数用含n的代数式分别表示为________和________,请用所学知识说明它们是一组勾股数.
查看答案和解析>>
科目:初中数学 来源: 题型:
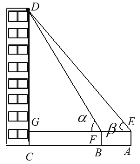
【题目】某兴趣小组用高为1米的仪器测量建筑物CD的高度.如示意图,由距CD一定距离的A处用仪器观察建筑物顶部D的仰角为∠β=30![]() ,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60
,在A和C之间选一点B,由B处用仪器观察建筑物顶部D的仰角为∠ɑ=60![]() .测得A,B之间的距离为4米,建筑物CD的高度为______ .
.测得A,B之间的距离为4米,建筑物CD的高度为______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
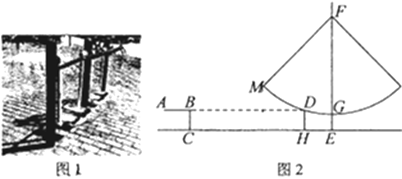
【题目】如图![]() 是某公园内健身的太空漫步机,当人踩在踏板上,握住扶手,两腿迈开到一定角度时的示意图如图
是某公园内健身的太空漫步机,当人踩在踏板上,握住扶手,两腿迈开到一定角度时的示意图如图![]() 所示,某个高
所示,某个高![]() 为
为![]() 分米的石凳旁边建一个太空漫步机,为方便行人通过,踏板与石凳之间保持了一定的距离,测得踏板静止时
分米的石凳旁边建一个太空漫步机,为方便行人通过,踏板与石凳之间保持了一定的距离,测得踏板静止时![]() 分米,
分米,![]() 分米,
分米,![]() 交
交![]() 于点
于点![]() ,
,![]() ,且
,且![]() ,则
,则![]() 的长为_____分米;
的长为_____分米;![]() 在旋转过程中,当点
在旋转过程中,当点![]() 与点
与点![]() 的距离最小时,此时点
的距离最小时,此时点![]() 到
到![]() 的距离为_______分米.
的距离为_______分米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校学生的身高情况,随机抽取该校男生、女生进行抽样调査.已知抽取的样本中,男生、女生的人数相同,利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
其中,C组男生的身高如下(单位:cm):
160 161 161 162 163 163 163 163 163 164
C组女生的身高如下(单位:cm):
160 160 161 161 161 161 162 162 163 164
根据图表提供的信息,回答下列问题:
(1)样本中,男生中位数为_________,女生身高在E组的人数有_________人;
(2)现有两名身高都为160cm的男生与女生,比较这两个同学分别在男生、女生中的身高情况,并简述理由;
(3)若已知该校共有男生400人,女生380人,请估计身高在![]() 之间的学生约有多少人?
之间的学生约有多少人?

身高情况分组表(单位:cm)
组别 | 身高/cm |
A |
|
B |
|
C |
|
D |
|
E |
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com