
ЁОЬтФПЁПМзЁЂввСНШЫдк1200УзГЄЕФжБЯпЕРТЗЩЯХмВНЃЌМзЁЂввСНШЫЭЌЦ№ЕуЁЂЭЌЗНЯђГіЗЂЃЌВЂЗжБ№вдВЛЭЌЕФЫйЖШдШЫйЧАНјЃЌвбжЊЃЌМзГіЗЂ30УыКѓЃЌввГіЗЂЃЌввЕНжеЕуКѓСЂМДЗЕЛиЃЌВЂвддРДЕФЫйЖШЧАНјЃЌзюКѓгыМзЯргіЃЌДЫЪБХмВННсЪјЃЎШчЭМЃЌyЃЈУзЃЉБэЪОМзЁЂввСНШЫжЎМфЕФОрРыЃЌxЃЈУыЃЉБэЪОМзГіЗЂЕФЪБМфЃЌЭМжаелЯпМАЪ§ОнБэЪОећИіХмВНЙ§ГЬжаyгыxКЏЪ§ЙиЯЕЃЌФЧУДЃЌввЕНДяжеЕуКѓ_____УыгыМзЯргіЃЎ
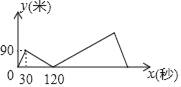
ЁОД№АИЁП30
ЁОНтЮіЁП
гЩЭМЯѓПЩвдVМзЃН![]() ЃН3m/sЃЌVзЗЃН
ЃН3m/sЃЌVзЗЃН![]() ЃН1m/sЃЌЙЪVввЃН1+3ЃН4m/sЃЌгЩДЫПЩЧѓЕУввзпЭъШЋГЬЫљгУЕФЪБМфЮЊЃК
ЃН1m/sЃЌЙЪVввЃН1+3ЃН4m/sЃЌгЩДЫПЩЧѓЕУввзпЭъШЋГЬЫљгУЕФЪБМфЮЊЃК![]() ЃН300sЃЌдђПЩвдЧѓЕУДЫЪБввгыМзЕФОрРыЃЌМДПЩЧѓГізюКѓгыМзЯргіЕФЪБМфЃЎ
ЃН300sЃЌдђПЩвдЧѓЕУДЫЪБввгыМзЕФОрРыЃЌМДПЩЧѓГізюКѓгыМзЯргіЕФЪБМфЃЎ
гЩЭМЯѓПЩЕУVМзЃН![]() ЃН3m/sЃЌVзЗЃН
ЃН3m/sЃЌVзЗЃН![]() ЃН1m/sЃЌ
ЃН1m/sЃЌ
ЁрVввЃН1+3ЃН4m/sЃЌ
ЁрввзпЭъШЋГЬЫљгУЕФЪБМфЮЊЃК![]() ЃН300sЃЌ
ЃН300sЃЌ
ДЫЪБМзЫљзпЕФТЗГЬЮЊЃКЃЈ300+30ЃЉЁС3ЃН990mЃЎ
ДЫЪБМзввЯрОрЃК1200Љ990ЃН210m
дђзюКѓЯргіЕФЪБМфЮЊЃК![]() ЃН30s
ЃН30s
ЙЪД№АИЮЊЃК30



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
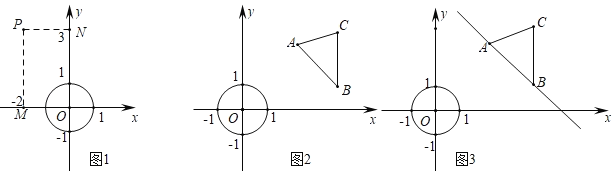
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyЃЌЖдгкЕуPЃЈxpЃЌypЃЉКЭЭМаЮGЃЌЩшQЃЈxQЃЌyQЃЉЪЧЭМаЮGЩЯШЮвтвЛЕуЃЌ|xpЉxQ|ЕФзюаЁжЕНаЕуPКЭЭМаЮGЕФЁАЫЎЦНОрРыЁБЃЌ|ypЉyQ|ЕФзюаЁжЕНаЕуPКЭЭМаЮGЕФЁАЪњжБОрРыЁБЃЌЕуPКЭЭМаЮGЕФЁАЫЎЦНОрРыЁБгыЁАЪњжБОрРыЁБЕФзюДѓжЕНазіЕуPКЭЭМаЮGЕФЁАОјЖдОрРыЁБ
Р§ШчЃКЕуPЃЈЉ2ЃЌ3ЃЉКЭАыОЖЮЊ1ЕФЁбOЃЌвђЮЊЁбOЩЯШЮвЛЕуQЃЈxQЃЌyQЃЉТњзуЉ1ЁмxQЁм1ЃЌЉ1ЁмyQЁм1ЃЌЕуPКЭЁбOЕФЁАЫЎЦНОрРыЁБЮЊ|Љ2ЉxQ|ЕФзюаЁжЕЃЌМД|Љ2ЉЃЈЉ1ЃЉ|=1ЃЌЕуPКЭЁбOЕФЁАЪњжБОрРыЁБЮЊ|3ЉyQ|ЕФзюаЁжЕМД|3Љ1|=2ЃЌвђЮЊ2ЃО1ЃЌЫљвдЕуPКЭЁбOЕФЁАОјЖдОрРыЁБЮЊ2ЃЎ
вбжЊЁбOАыОЖЮЊ1ЃЌAЃЈ2ЃЌ![]() ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЌCЃЈ4ЃЌ3ЃЉ
ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЌCЃЈ4ЃЌ3ЃЉ
ЃЈ1ЃЉЂйжБНгаДГіЕуAКЭЁбOЕФЁАОјЖдОрРыЁБ
ЂквбжЊDЪЧЁїABCБпЩЯвЛИіЖЏЕуЃЌЕБЕуDгыЁбOЕФЁАОјЖдОрРыЁБЮЊ2ЪБЃЌаДГівЛИіТњзуЬѕМўЕФЕуDЕФзјБъЃЛ
ЃЈ2ЃЉвбжЊEЪЧЁїABCБпвЛИіЖЏЕуЃЌжБНгаДГіЕуEгыЁбOЕФЁАОјЖдОрРыЁБЕФзюаЁжЕМАЯргІЕФЕуEЕФзјБъ
ЃЈ3ЃЉвбжЊPЪЧЁбOЩЯвЛИіЖЏЕуЃЌЁїABCбижБЯпABЦНвЦЙ§ГЬжаЃЌжБНгаДГіЕуPгыЁїABCЕФЁАОјЖдОрРыЁБЕФзюаЁжЕМАЯргІЕФЕуPКЭЕуCЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаИГгш![]() ЪЕМЪвтвхЕФа№ЪіжаВЛе§ШЗЕФЪЧЃЈ ЃЉ
ЪЕМЪвтвхЕФа№ЪіжаВЛе§ШЗЕФЪЧЃЈ ЃЉ
A. ШєЦЯЬбЕФМлИёЪЧ4дЊ/ЧЇПЫЃЌдђ![]() БэЪОТђ
БэЪОТђ![]() ЧЇПЫЦЯЬбЕФН№Жю
ЧЇПЫЦЯЬбЕФН№Жю
B. Шє![]() БэЪОвЛИіе§ЗНаЮЕФБпГЄЃЌдђ
БэЪОвЛИіе§ЗНаЮЕФБпГЄЃЌдђ![]() БэЪОетИіе§ЗНаЮЕФжмГЄ
БэЪОетИіе§ЗНаЮЕФжмГЄ
C. НЋвЛИіаЁФОПщЗХдкЫЎЦНзРУцЩЯЃЌШє4БэЪОаЁФОПщгызРУцЕФНгДЅУцЛ§ЃЌ![]() БэЪОзРУцЪмЕНЕФбЙЧПЃЌдђ
БэЪОзРУцЪмЕНЕФбЙЧПЃЌдђ![]() БэЪОаЁФОПщЖдзРУцЕФбЙСІ
БэЪОаЁФОПщЖдзРУцЕФбЙСІ
D. Шє4КЭ![]() ЗжБ№БэЪОвЛИіСНЮЛЪ§жаЕФЪЎЮЛЪ§зжКЭИіЮЛЪ§зжЃЌдђ
ЗжБ№БэЪОвЛИіСНЮЛЪ§жаЕФЪЎЮЛЪ§зжКЭИіЮЛЪ§зжЃЌдђ![]() БэЪОетИіСНЮЛЪ§
БэЪОетИіСНЮЛЪ§
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
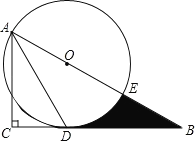
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌЁЯBACЕФНЧЦНЗжЯпADНЛBCБпгкDЃЎвдABЩЯФГвЛЕуOЮЊдВаФзїЁбOЃЌЪЙЁбOОЙ§ЕуAКЭЕуDЃЎ
ЃЈ1ЃЉХаЖЯжБЯпBCгыЁбOЕФЮЛжУЙиЯЕЃЌВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШєAC=3ЃЌЁЯB=30ЁуЃЎ
ЂйЧѓЁбOЕФАыОЖЃЛ
ЂкЩшЁбOгыABБпЕФСэвЛИіНЛЕуЮЊEЃЌЧѓЯпЖЮBDЁЂBEгыСгЛЁDEЫљЮЇГЩЕФвѕгАВПЗжЕФЭМаЮУцЛ§ЃЎЃЈНсЙћБЃСєИљКХКЭІаЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
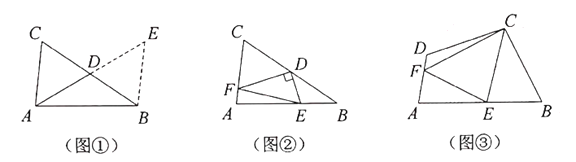
ЁОЬтФПЁПЃЈ1ЃЉдФЖСРэНтЃК
ШчЭМЂйЃЌдк![]() жаЃЌШє
жаЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() БпЩЯЕФжаЯп
БпЩЯЕФжаЯп![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ПЩвдгУШчЯТЗНЗЈЃКНЋ![]() ШЦзХЕу
ШЦзХЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕН
ЕУЕН![]() ЃЌдк
ЃЌдк![]() жаЃЌРћгУШ§НЧаЮШ§БпЕФЙиЯЕМДПЩХаЖЯжаЯп
жаЃЌРћгУШ§НЧаЮШ§БпЕФЙиЯЕМДПЩХаЖЯжаЯп![]() ЕФШЁжЕЗЖЮЇЪЧ______ЃЛ
ЕФШЁжЕЗЖЮЇЪЧ______ЃЛ
ЃЈ2ЃЉЮЪЬтНтОіЃК
ШчЭМЂкЃЌдк![]() жаЃЌ
жаЃЌ![]() ЪЧ
ЪЧ![]() БпЩЯЕФжаЕуЃЌ
БпЩЯЕФжаЕуЃЌ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌ
ЃЌ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ3ЃЉЮЪЬтЭиеЙЃК
ШчЭМЂлЃЌдкЫФБпаЮ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌвд
ЃЌвд![]() ЮЊЖЅЕузївЛИі
ЮЊЖЅЕузївЛИі![]() ЕФНЧЃЌНЧЕФСНБпЗжБ№НЛ
ЕФНЧЃЌНЧЕФСНБпЗжБ№НЛ![]() ЁЂ
ЁЂ![]() гк
гк![]() ЁЂ
ЁЂ![]() СНЕуЃЌСЌНг
СНЕуЃЌСЌНг![]() ЃЌЬНЫїЯпЖЮ
ЃЌЬНЫїЯпЖЮ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
жЎМфЕФЪ§СПЙиЯЕЃЌВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЋЫОЯњЪлСНжжвЮзгЃЌЦеЭЈвЮзгМлИёЪЧУПАб180дЊЃЌЪЕФОвЮзгЕФМлИёЪЧУПАб400дЊЃЎ
(1)ИУЙЋЫОдк2019ФъЕквЛдТЯњЪлСЫСНжжвЮзгЙВ900АбЃЌЯњЪлзмН№ЖюДяЕНСЫ272000дЊЃЌЧѓСНжжвЮСЫИїЯњЪлСЫЖрЩйАбЃП
(2)ЕкЖўдТе§КУИЯЩЯЪаРяПЊеЙМвОуеЙЯњЛюЖЏЃЌЙЋЫООіЖЈНЋЦеЭЈвЮзгУПАбНЕ30дЊКѓЯњЪлЃЌЪЕФОвЮзгУПАбНЕМл2a%(aЃО0)КѓЯњЪлЃЌдкеЙЯњЛюЖЏЕФЕквЛжмЃЌИУЙЋЫОЕФЦеЭЈвЮзгЯњЪлСПБШЩЯвЛдТШЋдТЦеЭЈвЮзгЕФЯњЪлСПЖрСЫ![]() a%ЃКЪЕФОвЮзгЕФЯњЪлСПБШЕквЛдТШЋдТЪЕФОвЮзгЕФЯњЪлСПЖрСЫa%ЃЌетвЛжмСНжжвЮзгЕФзмЯњЪлН№ЖюДяЕНСЫ251000дЊЃЌЧѓaЕФжЕЃЎ
a%ЃКЪЕФОвЮзгЕФЯњЪлСПБШЕквЛдТШЋдТЪЕФОвЮзгЕФЯњЪлСПЖрСЫa%ЃЌетвЛжмСНжжвЮзгЕФзмЯњЪлН№ЖюДяЕНСЫ251000дЊЃЌЧѓaЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
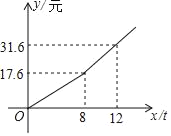
ЁОЬтФПЁПЮвЙњКмЖрГЧЪаЫЎзЪдДШБЗІЃЌЮЊСЫМгЧПОгУёЕФНкЫЎвтЪЖЃЌФГЪажЦЖЈСЫУПдТгУЫЎ8ЖжвдФкЃЈАќРЈ8ЖжЃЉКЭгУЫЎ8ЖжвдЩЯСНжжЪеЗбБъзМЃЈЪеЗбБъзМЃКУПЖжЫЎЕФМлИёЃЉЃЌФГгУЛЇУПдТгІНЛЫЎЗбyЃЈдЊЃЉЪЧгУЫЎСПxЃЈЖжЃЉЕФКЏЪ§ЃЌЦфКЏЪ§ЭМЯѓШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓГіздРДЫЎЙЋЫОдкетСНИігУЫЎЗЖЮЇФкЕФЪеЗбБъзМЃЛ
ЃЈ2ЃЉШєЗМЗММв6дТЗнЙВНЛЫЎЗб28.1дЊЃЌЧыаДГігУЫЎСПГЌЙ§8ЖжЪБгІНЛЫЎЗбyЃЈдЊЃЉгыгУЫЎСПxЃЈЖжЃЉжЎМфЕФКЏЪ§ЙиЯЕЃЌВЂЧѓГіЗМЗММв6дТЗнЕФгУЫЎСПЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжаЛЊірЪЧЙњМввЛМЖБЃЛЄЖЏЮяЃЌЫќЪЧДѓаЭфЇгЮадгуРрЃЌЩњдкГЄНЃЌГЄдкКЃбѓЃЌЪмЩњЬЌЛЗОГЕФгАЯьЃЌЪ§СПж№ФъЯТНЕЁЃжаЛЊірбаОПЫљУПФъЖЈЦкЭЈЙ§ШЫЙЄбјжГЗХСїРДдіМгжаЛЊірЕФЪ§СПЃЌУПФъЗХСїЕФжаЛЊіржагаЩйЪ§ЬхФкАВзАСЫГЄаЇЩљФХБъМЧЃЌБугкМьВтЫќУЧДгГЄНЕНКЃбѓЕФЪЪгІЧщПіЃЌетВПЗжжаЛЊірМђГЦЮЊЁАЩљФХірЁБЃЌбаОПЫљЪеМЏСЫЫќУЧЕНДяЯТгЮМрВтЕуAЕФЪБМфtЃЈhЃЉЕФЯрЙиЪ§ОнЃЌВЂжЦзїШчЯТВЛЭъећЭГМЦЭМКЭЭГМЦБэЃЎ
вбжЊЃКНёФъКЭШЅФъЗжБ№га20ЮВЁАЩљФХірЁБдкЗХСїЕФ96аЁЪБФкЕНДяМрВтЕуAЃЌНёФъТфдк24<tЁм48ФкЕФЁАЩљФХірЁББШШЅФъЖр1ЮВЃЌНёФъТфдк48<tЁм72ФкЕФЪ§ОнЗжБ№ЮЊ49ЃЌ60ЃЌ68ЃЌ68ЃЌ71ЃЎ
ШЅФъ20ЮВЁАЩљФХірЁБЕНДяМрВтЕуA ЫљгУЪБМфtЃЈhЃЉЕФЩШаЮЭГМЦЭМ
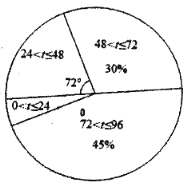
НёФъ20ЮВЁАЩљФХірЁБЕНДяМрВтЕуAЫљгУЪБМфtЃЈhЃЉЕФЦЕЪ§ЗжВМжБЗНЭМ
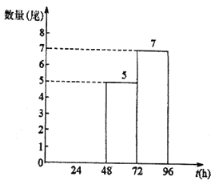
ЙигкЁАЩљФХірЁБЕНДяМрВтЕуAЫљгУЪБМфtЃЈhЃЉЕФЭГМЦБэ
ЦНОљЪ§ | жаЮЛЪ§ | жкЪ§ | ЗНВю | |
ШЅФъ | 64.2 | 68 | 73 | 715.6 |
НёФъ | 56.2 | a | 68 | 629.7 |
ЃЈ1ЃЉЧыВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЌВЂИљОнвдЩЯаХЯЂЬюПеЃКa= ЃЛ
ЃЈ2ЃЉжаЛЊірЕНДяКЃбѓЕФЪБМфдНПьЃЌЫЕУїЫќДгГЄНЕНКЃбѓЕФЪЪгІЧщПіОЭдНКУЃЌЧыИљОнЩЯЪіаХЯЂЃЌбЁдёвЛИіЭГМЦСПЫЕУїШЅФъКЭНёФъжаФФвЛФъжаЛЊірДгГЄНЕНКЃбѓЕФЪЪгІЧщПіИќКУЃЛ
ЃЈ3ЃЉШЅФъКЭНёФъИУЗХСїЕуЙВЗХСї1300ЮВжаЛЊірЃЌЦфжаЁАЩљФХірЁБЙВга50ЮВЃЌЧыЙРМЦНёФъКЭШЅФъдкЗХСї72аЁЪБФкЙВгаЖрЩйЮВжаЛЊірЭЈЙ§МрВтеОAЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
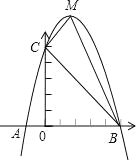
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§y=ax2+bx+cЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌЦфжаAЕузјБъЮЊЃЈЉ1ЃЌ0ЃЉЃЌЕуCЃЈ0ЃЌ5ЃЉЃЌСэХзЮяЯпОЙ§ЕуЃЈ1ЃЌ8ЃЉЃЌMЮЊЫќЕФЖЅЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїMCBЕФУцЛ§![]() ЃЎ
ЃЎ
ЃЈ3ЃЉдкзјБъжсЩЯЃЌЪЧЗёДцдкЕуNЃЌТњзуЁїBCNЮЊжБНЧШ§НЧаЮЃПШчДцдкЃЌЧыжБНгаДГіЫљгаТњзуЬѕМўЕФЕуNЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com