
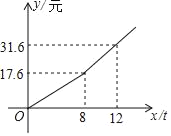
����Ŀ���ҹ��ܶ����ˮ��Դȱ����Ϊ�˼�ǿ����Ľ�ˮ��ʶ��ij���ƶ���ÿ����ˮ8�����ڣ�����8�֣�����ˮ8�����������շѱ����շѱ���ÿ��ˮ�ļ۸�ij�û�ÿ��Ӧ��ˮ��y��Ԫ������ˮ��x���֣��ĺ������亯��ͼ����ͼ��ʾ��
��1���������ˮ��˾����������ˮ��Χ�ڵ��շѱ���
��2����������6�·ݹ���ˮ��28.1Ԫ����д����ˮ������8��ʱӦ��ˮ��y��Ԫ������ˮ��x���֣�֮��ĺ�����ϵ�������������6�·ݵ���ˮ����
���𰸡���1��2.2��3.5��2��11
��������
��1�������ڲ�ͬ��Χ�ڵĺ����Ľ���ʽ��֪����0��8�ַ�Χ�ڣ�ÿ��2.2Ԫ����x��8ʱ��ÿ��ˮ3.5Ԫ��
��2��������֪������֪�����û��Ľ�ˮ�ѷ�Χ����x��8�ķ�Χ���������ʽ���ɵõ��𰸣�
�⣺��1��8�������շѱ���17.6��8��2.2Ԫ��
8�������շѱ�����31.6��17.6���£�12��8����3.5Ԫ��
��2���������֪��
y��3.5��x��8��+2.2��8
����y��3.5x��10.4
��y��28.1ʱ���У�3.5x��10.4��28.1
��x��11
�𣺷�����6�·���ˮ��Ϊ11�֣�


 һ����ʦ�����Ծ�ϵ�д�
һ����ʦ�����Ծ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�Ȼ��ش�����.�ڽ��ж��θ�ʽȥ��ʱ��������ʱ��������![]() ��
�� ![]() ��
�� ![]() һ����ʽ�ӣ���ʵ���ǻ����Խ����һ������
һ����ʽ�ӣ���ʵ���ǻ����Խ����һ������
![]() ��
��![]() ��һ��
��һ��
![]() ��
��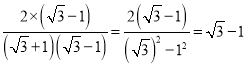 ������
������
�������ֻ���IJ��������ĸ������.
![]() �����������·�������
�����������·�������
![]() ��
�� ������
������
���ò�ͬ�ķ�������![]() .
.
��1�����գ�����ʽ��![]() ��______________________________________________��
��______________________________________________��
��2�����գ�����ʽ��![]() ��_________________________________________��
��_________________________________________��
��3������![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
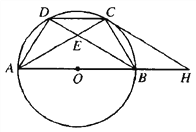
����Ŀ����ͼ����A��B��C��D��ֱ��ΪAB�ġ�O�ϵ��ĸ��㣬CD��BC��AC��BD���ڵ�E��
��1����֤��DC2��CE��AC��
��2����AE��2EC����![]() ֵ֮��
ֵ֮��
��3���ڣ�2���������£�����C����O�����ߣ���AB���ӳ����ڵ�H����S��ACH��![]() ����EC֮��.
����EC֮��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�������450ǧ�ף�����֮����һ������վO����AO��270ǧ�ף�һ���γ���A�س�������ÿСʱ90ǧ���ٶȿ���B�أ�һ���ͳ���B�س�������ÿСʱ60ǧ���ٶȿ���A�أ�����ͬʱ�����������ʱ��ΪtСʱ��
��1��������Сʱ����������
��2��������2Сʱʱ���γ��Ϳͳ��ֱ�������վO��Զ��
��3��������Сʱ���������50ǧ�ף�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʶ�ı����ˣ��Ƽ������������������Сѧÿ�궼Ҫ�ٰ�һ��Ƽ��˶��ᣮ��ͼΪ����ijУ2009��μӿƼ��˶��ẽģ������������ģ����ģ����ģ����ģ�ĸ���𣩵IJ�������ͳ��ͼ��
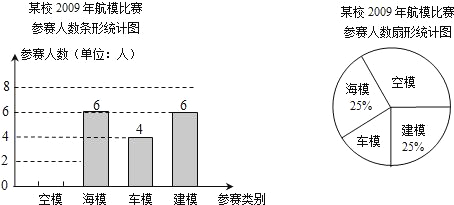
��1����У�μӳ�ģ����ģ�����������ֱ��� �˺� �ˣ�
��2����У�μӺ�ģ�������������� �ˣ���ģ�������ε�Բ�ĽǵĶ����� �㣬��������ͳ��ͼ��������������ܰ��ʾ����ͼʱ��������0.5�������ϵĺ�ɫǩ�ֱ�Ϳ�ڣ�
��3����ȫ����Сѧ�μӺ�ģ����ѡ���������ȡ80�ˣ�������32�˻�����������Сѧ�μӺ�ģ������������2485�ˣ�����������μӺ�ģ�����Ļ�����Լ�Ƕ����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ɸ���ͬ�IJ�Ϊ����������ij��������������. �磺2��2��2��(-3)��(-3)��(-3 )��( -3)��. ����������ij˷������ǰ� 2��2��2 ���� 2����������2 ��Ȧ 3 �η���. (-3)��(-3)��(-3 )��( -3)����(-3)����������-3 ��Ȧ 4 �η���.
һ��أ���![]() ��a��0������a��������a ��Ȧc�η���.
��a��0������a��������a ��Ȧc�η���.
(1)ֱ��д����������2��= ��(-3)�� = ��![]() ��= .
��= .
(2)���� 24��23 + (-8)��2��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��������A��B��C���㣬��A�͵�B���20����λ�����ҵ�A��B��ʾ����������Ϊ�෴����AC��36����������һ����P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����������յ�C�ƶ������ƶ�ʱ��Ϊt�룮
![]()
��1����A��ʾ������������ ������B��ʾ������������ ������C��ʾ������������ ����
��2������P�˶�����Bʱ����Q�ӵ�O��������ÿ��6����λ���ȵ��ٶ��������ڵ�O�͵�C֮�������˶���
����tΪ��ֵʱ����Q��һ�����P�غϣ�
�ڵ���P�˶�����Cʱ����Q���˶�ֹͣ�����ʱ��Qһ���˶��˶��ٸ���λ���ȣ��������ʱ��Q������������ʾ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
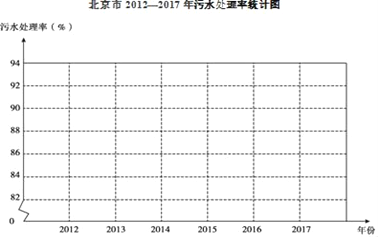
����Ŀ�������л�����չ���л������裬������ˮ�������ص㹤��֮һ�������DZ�����2012��2017����ˮ������ͳ�Ʊ���
��� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
��ˮ�����ʣ�%�� | 83.0 | 84.6 | 86.1 | 87.9 | 90.0 | 92.0 |
��1��������ͼ��2012��2017�걱������ˮ�����ʱ�ʾ����������ͼ�б�����Ӧ�����ݣ�
��2������ͳ��ͼ�����ṩ����Ϣ��Ԥ��2018�걱������ˮ������ԼΪ_____%��˵�����Ԥ�����ɣ�_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧ�������εĸߺ�С������������������������о�����ͼ��![]() ��
��![]() �б�
�б�![]() �ϵ�-�㣬����
�ϵ�-�㣬����![]() ��
��![]() �ֱ�����
�ֱ�����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() �����֮�͵���
�����֮�͵���![]() ��������е�����ϵʽ��
��������е�����ϵʽ��![]() .����������ͬһƽ��ͼ�ε������������;�����Եó�����߶ε�������ϵʽ���Ӷ����ڽ����ѧ����ķ�����Ϊ���Ȼ������������볢�������ַ��������������.
.����������ͬһƽ��ͼ�ε������������;�����Եó�����߶ε�������ϵʽ���Ӷ����ڽ����ѧ����ķ�����Ϊ���Ȼ������������볢�������ַ��������������.



ͼ(1) ͼ(2)
(1)��ͼ(1)�� ����![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() ��һ�㣬����
��һ�㣬����![]() ��
��![]() ��
��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ��
��![]() ����
����![]() ��ֵ��
��ֵ��
(2)��ͼ(2)����![]() �У���ƽ����
�У���ƽ����![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() �ֱ���
�ֱ���![]() ��
��![]() ������ֱ�Ϊ��
������ֱ�Ϊ��![]() ��
��![]() ����
����![]() ��
��![]() �����ı���
�����ı���![]() ���ܳ�.
���ܳ�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com