
【题目】直线AB交⊙O于C、D两点,CE是⊙O的直径,CF平分∠ACE交⊙O于点F,连接EF,过点F作FG∥ED交AB于点G.
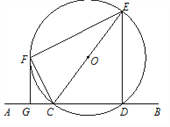
(1)求证:直线FG是⊙O的切线;
(2)若FG=4,⊙O的半径为5,求四边形FGDE的面积.
【答案】(1)证明见解析(2)48
【解析】试题分析:(1)利用角平分线的性质以及等腰三角形的性质得出∠OFC=∠FCG,继而得出∠GFC+∠OFC=90°,即可得出答案;
(2)首先得出四边形FGDH是矩形,进而利用勾股定理得出HO的长,进而得出答案.
试题解析:(1)连接FO,
∵ OF=OC,
∴ ∠OFC=∠OCF.
∵CF平分∠ACE,
∴∠FCG=∠FCE.
∴∠OFC=∠FCG.
∵ CE是⊙O的直径,
∴∠EDG=90°,
又∵FG∥ED,
∴∠FGC=180°-∠EDG=90°,
∴∠GFC+∠FCG=90°
∴∠GFC+∠OFC=90°,
即∠GFO=90°,
∴OF⊥GF,
又∵OF是⊙O半径,
∴FG与⊙O相切.
(2)延长FO,与ED交于点H,
由(1)可知∠HFG=∠FGD=∠GDH=90°,
∴四边形FGDH是矩形.
∴FH⊥ED,
∴HE=HD.
又∵四边形FGDH是矩形,FG=HD,
∴HE=FG=4.
∴ED=8.
∵在Rt△OHE中,∠OHE=90°,
∴OH=OE2-HE2=52-42=3.
∴FH=FO+OH=5+3=8.
S四边形FGDH=12(FG+ED)FH=12×(4+8)×8=48.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:
【题目】如图,数轴上,点![]() 的初始位置表示的数为
的初始位置表示的数为![]() ,现点
,现点![]() 做如下移动:第
做如下移动:第![]() 次点
次点![]() 向左移动
向左移动![]() 个单位长度至点
个单位长度至点![]() ,第
,第![]() 次从点
次从点![]() 向右移动
向右移动![]() 个单位长度至点
个单位长度至点![]() ,第
,第![]() 次从点
次从点![]() 向左移动
向左移动![]() 个单位长度至点
个单位长度至点![]() ,
, ![]() ,按照这种移动方式进行下去,如果点
,按照这种移动方式进行下去,如果点![]() 与原点的距离不小于
与原点的距离不小于![]() ,那么
,那么![]() 的最小值是__________.
的最小值是__________.
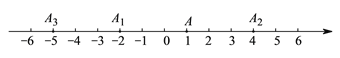
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的个数是( )
(1)能够完全重合的两个图形全等;
(2)两边和一角对应相等的两个三角形全等;
(3)两角和一边对应相等的两个三角形全等;
(4)全等三角形对应边相等.
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() 的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n).
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(﹣4,n). 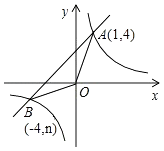
(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是一个长为2a、宽为2b的长方形(其中a,b均为正数,且a>b),沿图中虚线用剪刀均匀分成四块相同小长方形,然后按图2方式拼成一个大正方形.
(1)你认为图2中大正方形的边长为 a+b ;小正方形(阴影部分)的边长为 .(用含a、b的代数式表示)
(2)仔细观察图2,请你写出下列三个代数式:(a+b)2,(a-b)2,ab所表示的图形面积之间的相等关系,并选取适合a、b的数值加以验证.
(3)已知a+b=7,ab=6.求代数式(a-b)的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
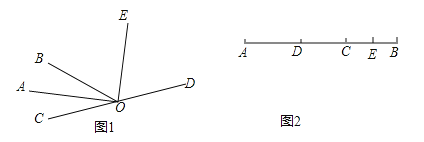
【题目】(1)如图1,已知O是直线CD上的点,OA平分∠BOC,OE平分∠BOD,∠AOC=35°,求∠BOE,∠COE的度数.
(2)如图2,已知AB=16cm,C是AB上一点,点D是线段AC的中点,点E是线段BC的中点,求线段DE的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com