
°æƒø°ø°∞∂ÀŒÁΩ⁄°± «Œ“π˙µƒ¥´Õ≥º—Ω⁄£¨√Òº‰¿˙¿¥”–≥‘°∞Ù’◊”°±µƒœ∞À◊£ÆŒ“ –ƒ≥ ≥∆∑≥ߌ™¡ÀΩ‚ –√Ò∂‘»•ƒÍœ˙¡øΩœ∫√µƒ»‚œ⁄Ù’°¢∂π…≥œ⁄Ù’°¢∫Ï‘Êœ⁄Ù’°¢µ∞ª∆œ⁄Ù’£®“‘œ¬∑÷±”√A£¨B£¨C£¨D±Ì 棩’‚Àƒ÷÷≤ªÕ¨ø⁄Œ∂Ù’◊”µƒœ≤∞Æ«Èøˆ£¨‘⁄Ω⁄«∞∂‘ƒ≥æ”√Ò«¯ –√ÒΩ¯––¡À≥È—˘µ˜≤È£¨≤¢Ω´µ˜≤È«ÈøˆªÊ÷∆≥…»Áœ¬¡Ω∑˘Õ≥º∆Õº
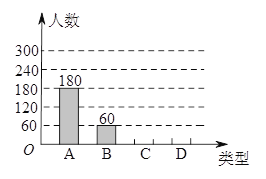
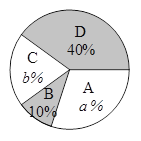
«Î∏˘æð“‘…œ–≈œ¢ªÿ¥£∫
£®1£©±æ¥Œ≤Œº”≥È—˘µ˜≤ȵƒæ”√Ò”–________»À£ª
£®2£©…»–ŒÕ≥º∆Õº÷–£∫a=________£¨b=_________£¨≤¢∞—Ãı–ŒÕ≥º∆Õº≤π≥‰ÕÍ’˚£ª
£®3£©»Ù”–Õ‚–ÕÕÍ»´œýÕ¨µƒA£¨B£¨C£¨DÙ’∏˜“ª∏ˆ£¨÷Û Ï∫Û£¨–°Õı≥‘¡À¡Ω∏ˆ£¨”√¡–±ÌªÚª≠ ˜◊¥Õºµƒ∑Ω∑®£¨«ÛÀ˚µ⁄∂˛∏ˆ≥‘µΩµƒ«°∫√ «CÙ’µƒ∏≈¬ £Æ
°æ¥∞∏°ø£®1£©600.£®2£©30£ª20;≤πÕºº˚Ω‚Œˆ£ª£®3£©![]() £Æ
£Æ
°æΩ‚Œˆ°ø
‘£®1£©”√B–°◊ȵƒ∆µ ˝≥˝“‘B–°◊ÈÀ˘’ºµƒ∞Ÿ∑÷±»º¥ø…«Ûµ√Ω·¬€£ª
£®2£©∑÷±«Ûµ√A◊È∫ÕC–°◊ȵƒ∆µ ˝º∞∆‰À˘’ºµƒ∞Ÿ∑÷±»º¥ø…≤π»´Õ≥º∆Õº£ª
£®3£©¡–≥ˆ ˜◊¥Õºº¥ø…«Ûµ√Ω·¬€£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©60°¬10%=600£®»À£©£Æ
¥£∫±æ¥Œ≤Œº”≥È—˘µ˜≤ȵƒæ”√Ò”–600»À£Æ
£®2£©180°¬600=0.3=30%
°ýa=30
C–°◊ÈÀ˘’ºµƒ±»¿˝Œ™£∫1-40%-10%-30%=20%
°ýb=20.
D–°◊ȵƒ»À ˝Œ™£∫600°¡40%=240»À.
≤πÕº»Áœ¬£∫
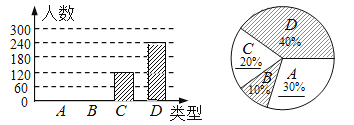
£®3£©»ÁÕº£∫
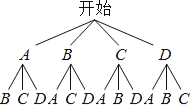
P£®CÙ’£©=![]() £Æ
£Æ
¥£∫À˚µ⁄∂˛∏ˆ≥‘µΩµƒ«°∫√ «CÙ’µƒ∏≈¬ «![]() £Æ
£Æ


 —Ùπ‚øŒÃ√øŒ ±”≈ªØ◊˜“µœµ¡–¥∞∏
—Ùπ‚øŒÃ√øŒ ±”≈ªØ◊˜“µœµ¡–¥∞∏
| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
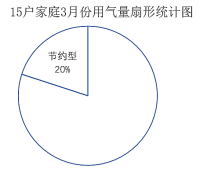
°æƒø°øµ˜≤È◊˜“µ£∫¡ÀΩ‚ƒ„À˘◊°–°«¯º“Õ•3‘¬∑ð”√∆¯¡ø«Èøˆ£Æ
–°ÃÏ°¢–°∂´∫Õ–°Ðø»˝ŒªÕ¨—ß◊°‘⁄Õ¨“ª–°«¯£¨∏√–°«¯π≤”–300ªßº“Õ•£¨√øªßº“Õ•»À ˝‘⁄2°™5÷ƺ‰£¨’‚300ªßº“Õ•µƒ∆Ωæ˘»À ˝‘ºŒ™3.3£Æ
–°ÃÏ°¢–°∂´∫Õ–°Ðø∏˜◊‘∂‘∏√–°«¯º“Õ•3‘¬∑ð”√∆¯¡ø«ÈøˆΩ¯––¡À≥È—˘µ˜≤È£¨Ω´ ’ºØµƒ ˝æðΩ¯––¡À’˚¿Ì£¨ªÊ÷∆µƒÕ≥º∆±Ì∑÷±Œ™±Ì1°¢±Ì2°¢±Ì3£¨
±Ì1≥È—˘µ˜≤È–°«¯4ªßº“Õ•3‘¬∑ð”√∆¯¡øÕ≥º∆±Ì£®µ•Œª£∫![]() £©
£©
º“Õ•»À ˝ | 2 | 3 | 4 | 5 |
”√∆¯¡ø | 14 | 19 | 21 | 26 |
±Ì2≥È—˘µ˜≤È–°«¯15ªßº“Õ•3‘¬∑ð”√∆¯¡øÕ≥º∆±Ì£®µ•Œª£∫![]() £©
£©
º“Õ•»À ˝ | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 4 |
”√∆¯¡ø | 10 | 11 | 15 | 13 | 14 | 15 | 17 | 17 | 18 | 18 | 18 | 18 | 18 | 20 | 22 |
±Ì3≥È—˘µ˜≤È–°«¯15ªßº“Õ•3‘¬∑ð”√∆¯¡øÕ≥º∆±Ì£®µ•Œª£∫![]() £©
£©
º“Õ•»À ˝ | 2 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 | 5 | 5 |
”√∆¯¡ø | 10 | 12 | 13 | 14 | 17 | 17 | 18 | 20 | 20 | 21 | 22 | 26 | 31 | 28 | 31 |
∏˘æð“‘…œ≤ƒ¡œªÿ¥Œ £∫
£®1£©–°ÃÏ°¢–°∂´∫Õ–°Ðø»˝»À÷–£¨ƒƒ“ªŒªÕ¨—ß≥È—˘µ˜≤ȵƒ ˝æðƒÐΩœ∫√µÿ∑¥”¶≥ˆ∏√–°«¯º“Õ•3‘¬∑ð”√∆¯¡ø«Èøˆ£ø«ÎºÚ“™Àµ√˜∆‰À˚¡ΩŒªÕ¨—ß≥È—˘µ˜≤ȵƒ≤ª◊„÷Æ¥¶£ª
£®2£©–°∂´Ω´±Ì2÷–µƒ ˝æð∞¥”√∆¯¡ø![]() ¥Û–°∑÷Œ™»˝¿ý£ª
¥Û–°∑÷Œ™»˝¿ý£ª
¢ŸΩ⁄‘º–Õ£∫![]() £ª
£ª
¢⁄æ”÷––Õ£∫![]() £ª
£ª
¢€∆´∏þ–Õ£∫![]() £ª≤¢ªÊ÷∆≥…»Áœ¬…»–ŒÕ≥º∆Õº£¨«Î∞Ô÷˙À˚Ω´…»–ŒÕº≤π≥‰ÕÍ’˚£ª
£ª≤¢ªÊ÷∆≥…»Áœ¬…»–ŒÕ≥º∆Õº£¨«Î∞Ô÷˙À˚Ω´…»–ŒÕº≤π≥‰ÕÍ’˚£ª
£®3£©–°ÐøÀ„≥ˆ±Ì3÷–3‘¬∑ð∆Ωæ˘√ø»Àµƒ”√¡øŒ™![]() £¨«Îπ¿º∆∏√–°«¯3‘¬∑ðµƒ◊Д√∆¯¡ø£Æ
£¨«Îπ¿º∆∏√–°«¯3‘¬∑ðµƒ◊Д√∆¯¡ø£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
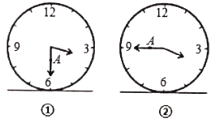
°æƒø°øÕº¢Ÿ±Ì 擪∏ˆ ±÷”µƒ÷”√Ê¥π÷±πÃ∂®”⁄ÀÆ∆Ω◊¿√Ê…œ£¨∆‰÷–∑÷’Î…œ”–“ªµ„A£¨µ±÷”√Êœ‘ æ3µ„30∑÷ ±£¨∑÷’Î¥π÷±”⁄◊¿√Ê£¨Aµ„æý◊¿√ʵƒ∏þ∂»Œ™10cm£ÆÕº¢⁄±Ì æµ±÷”√Êœ‘ æ3µ„45∑÷ ±£¨Aµ„æý◊¿√ʵƒ∏þ∂»Œ™16cm£¨»Ù÷”√Êœ‘ æ3µ„55∑÷ ±£¨Aµ„æý◊¿√ʵƒ∏þ∂»Œ™____![]() £Æ
£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–£¨∫Ø ˝y![]() £®x£æ0£©µƒÕºœÛ”Î÷±œþy=2x+1Ωª”⁄µ„A£®1£¨m£©
£®x£æ0£©µƒÕºœÛ”Î÷±œþy=2x+1Ωª”⁄µ„A£®1£¨m£©
£®1£©«Ûk£¨mµƒ÷µ£ª
£®2£©“—÷™µ„P£®0£¨n£©£®n£æ0£©£¨π˝µ„P◊˜∆Ω––”⁄x÷·µƒ÷±œþ£¨Ωª÷±œþy=2x+1”⁄µ„B£¨Ωª∫Ø ˝y![]() £®x£æ0£©µƒÕºœÛ”⁄µ„C£Æ∫·°¢◊ð◊¯±Í∂º «’˚ ˝µƒµ„Ω–◊ˆ’˚µ„£Æ
£®x£æ0£©µƒÕºœÛ”⁄µ„C£Æ∫·°¢◊ð◊¯±Í∂º «’˚ ˝µƒµ„Ω–◊ˆ’˚µ„£Æ
¢Ÿµ±n=1 ±£¨–¥≥ˆœþ∂ŒBC…œµƒ’˚µ„µƒ◊¯±Í£ª
¢⁄»Ùy![]() £®x£æ0£©µƒÕºœÛ‘⁄µ„A£¨C÷ƺ‰µƒ≤ø∑÷”Îœþ∂ŒAB£¨BCÀ˘Œß≥…µƒ«¯”Úƒ⁄£®∞¸¿®±þΩÁ£©«°”–6∏ˆ’˚µ„£¨÷±Ω”–¥≥ˆnµƒ»°÷µ∑∂Œß£Æ
£®x£æ0£©µƒÕºœÛ‘⁄µ„A£¨C÷ƺ‰µƒ≤ø∑÷”Îœþ∂ŒAB£¨BCÀ˘Œß≥…µƒ«¯”Úƒ⁄£®∞¸¿®±þΩÁ£©«°”–6∏ˆ’˚µ„£¨÷±Ω”–¥≥ˆnµƒ»°÷µ∑∂Œß£Æ
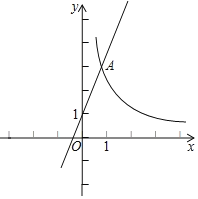
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
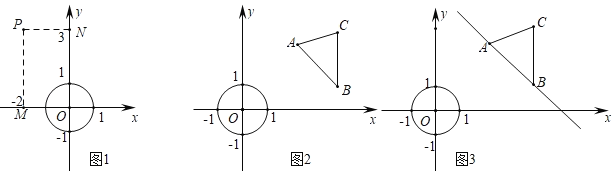
°æƒø°ø‘⁄∆Ω√Ê÷±Ω«◊¯±ÍœµxOy£¨∂‘”⁄µ„P£®xp£¨yp£©∫ÕÕº–ŒG£¨…ËQ£®xQ£¨yQ£© «Õº–ŒG…œ»Œ“‚“ªµ„£¨|xp©ÅxQ|µƒ◊Ó–°÷µΩ–µ„P∫ÕÕº–ŒGµƒ°∞ÀÆ∆Ωæý¿Î°±£¨|yp©ÅyQ|µƒ◊Ó–°÷µΩ–µ„P∫ÕÕº–ŒGµƒ°∞ ˙÷±æý¿Î°±£¨µ„P∫ÕÕº–ŒGµƒ°∞ÀÆ∆Ωæý¿Î°±”ΰ∞ ˙÷±æý¿Î°±µƒ◊Ó¥Û÷µΩ–◊ˆµ„P∫ÕÕº–ŒGµƒ°∞æ¯∂‘æý¿Î°±
¿˝»Á£∫µ„P£®©Å2£¨3£©∫Õ∞Îæ∂Œ™1µƒ°—O£¨“ÚŒ™°—O…œ»Œ“ªµ„Q£®xQ£¨yQ£©¬˙◊„©Å1°ÐxQ°Ð1£¨©Å1°ÐyQ°Ð1£¨µ„P∫Õ°—Oµƒ°∞ÀÆ∆Ωæý¿Î°±Œ™|©Å2©ÅxQ|µƒ◊Ó–°÷µ£¨º¥|©Å2©Å£®©Å1£©|=1£¨µ„P∫Õ°—Oµƒ°∞ ˙÷±æý¿Î°±Œ™|3©ÅyQ|µƒ◊Ó–°÷µº¥|3©Å1|=2£¨“ÚŒ™2£æ1£¨À˘“‘µ„P∫Õ°—Oµƒ°∞æ¯∂‘æý¿Î°±Œ™2£Æ
“—÷™°—O∞Îæ∂Œ™1£¨A£®2£¨![]() £©£¨B£®4£¨1£©£¨C£®4£¨3£©
£©£¨B£®4£¨1£©£¨C£®4£¨3£©
£®1£©¢Ÿ÷±Ω”–¥≥ˆµ„A∫Õ°—Oµƒ°∞æ¯∂‘æý¿Î°±
¢⁄“—÷™D «°˜ABC±þ…œ“ª∏ˆ∂ص„£¨µ±µ„D”ΰ—Oµƒ°∞æ¯∂‘æý¿Î°±Œ™2 ±£¨–¥≥ˆ“ª∏ˆ¬˙◊„Ãıº˛µƒµ„Dµƒ◊¯±Í£ª
£®2£©“—÷™E «°˜ABC±þ“ª∏ˆ∂ص„£¨÷±Ω”–¥≥ˆµ„E”ΰ—Oµƒ°∞æ¯∂‘æý¿Î°±µƒ◊Ó–°÷µº∞œý”¶µƒµ„Eµƒ◊¯±Í
£®3£©“—÷™P «°—O…œ“ª∏ˆ∂ص„£¨°˜ABC—ÿ÷±œþAB∆Ω“∆π˝≥Ã÷–£¨÷±Ω”–¥≥ˆµ„P”ΰ˜ABCµƒ°∞æ¯∂‘æý¿Î°±µƒ◊Ó–°÷µº∞œý”¶µƒµ„P∫Õµ„Cµƒ◊¯±Í£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
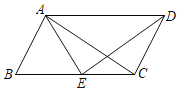
°æƒø°ø»ÁÕº£¨‘⁄∆Ω––Àƒ±þ–ŒABCD÷–£¨AB£ΩAE£Æ»ÙAE∆Ω∑÷°œDAB£¨°œEAC£Ω25°„£¨‘Ú°œB£Ω_____£¨°œAEDµƒ∂» ˝Œ™_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨≈◊ŒÔœþy=ax2+(4a©Å1)x©Å4”Îx÷·Ωª”⁄µ„A°¢B£¨”Îy÷·Ωª”⁄µ„C£¨«“OC=2OB£¨µ„DŒ™œþ∂ŒOB…œ“ª∂ص„(≤ª”ε„B÷ÿ∫œ)£¨π˝µ„D◊˜æÿ–ŒDEFH£¨µ„H°¢F‘⁄≈◊ŒÔœþ…œ£¨µ„E‘⁄x÷·…œ£Æ
£®1£©«Û≈◊ŒÔœþµƒΩ‚Œˆ Ω£ª
£®2£©µ±æÿ–ŒDEFHµƒ÷Ð≥§◊Ó¥Û ±£¨«Ûæÿ–ŒDEFHµƒ√ʪ˝£ª
£®3£©‘⁄£®2£©µƒÃıº˛œ¬£¨æÿ–ŒDEFH≤ª∂Ø£¨Ω´≈◊ŒÔœþ—ÿ◊≈x÷·œÚ◊Û∆Ω“∆m∏ˆµ•Œª£¨≈◊ŒÔœþ”Îæÿ–ŒDEFHµƒ±þΩª”⁄µ„M°¢N£¨¡¨Ω”M°¢N£Æ»ÙMN«°∫√∆Ω∑÷æÿ–ŒDEFHµƒ√ʪ˝£¨«Ûmµƒ÷µ£Æ

≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»Ùπÿ”⁄xµƒ“ª‘™∂˛¥Œ∑Ω≥Ã3x2£´3(a£´b)x£´4ab£Ω0µƒ¡Ω∏ˆ µ ˝∏˘x1°¢x2¬˙◊„πÿœµ Ω£∫x1(x1£´1)£´x2(x2£´1)£Ω(x1£´1)(x2£´1)£Æ≈–∂œ(a£´b)2°Ð4 «∑Ò’˝»∑£¨»Ù’˝»∑£¨«Îº”“‘÷§√˜£ª»Ù≤ª’˝»∑£¨«Î染ª∑¥¿˝£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥π´Àæœ˙ €¡Ω÷÷“Œ◊”£¨∆’Õ®“Œ◊”º€∏Ò «√ø∞—180‘™£¨ µƒæ“Œ◊”µƒº€∏Ò «√ø∞—400‘™£Æ
(1)∏√π´Àæ‘⁄2019ƒÍµ⁄“ª‘¬œ˙ €¡À¡Ω÷÷“Œ◊”π≤900∞—£¨œ˙ €◊ÐΩ∂Ó¥ÔµΩ¡À272000‘™£¨«Û¡Ω÷÷“Œ¡À∏˜œ˙ €¡À∂ý…Ÿ∞—£ø
(2)µ⁄∂˛‘¬’˝∫√∏œ…œ –¿Ôø™’πº“æ„’πœ˙ªÓ∂Ø£¨π´Àææˆ∂®Ω´∆’Õ®“Œ◊”√ø∞—Ωµ30‘™∫Ûœ˙ €£¨ µƒæ“Œ◊”√ø∞—Ωµº€2a%(a£æ0)∫Ûœ˙ €£¨‘⁄’πœ˙ªÓ∂صƒµ⁄“ª÷У¨∏√π´À浃∆’Õ®“Œ◊”œ˙ €¡ø±»…œ“ª‘¬»´‘¬∆’Õ®“Œ◊”µƒœ˙ €¡ø∂ý¡À![]() a%£∫ µƒæ“Œ◊”µƒœ˙ €¡ø±»µ⁄“ª‘¬»´‘¬ µƒæ“Œ◊”µƒœ˙ €¡ø∂ý¡Àa%£¨’‚“ª÷СΩ÷÷“Œ◊”µƒ◊Ðœ˙ €Ω∂Ó¥ÔµΩ¡À251000‘™£¨«Ûaµƒ÷µ£Æ
a%£∫ µƒæ“Œ◊”µƒœ˙ €¡ø±»µ⁄“ª‘¬»´‘¬ µƒæ“Œ◊”µƒœ˙ €¡ø∂ý¡Àa%£¨’‚“ª÷СΩ÷÷“Œ◊”µƒ◊Ðœ˙ €Ω∂Ó¥ÔµΩ¡À251000‘™£¨«Ûaµƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com