
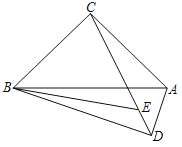
【题目】如图,等腰直角△ABC的斜边AB下方有一动点D,∠ADB=90°,BE平分∠ABD交CD于点E,则![]() 的最小值是_____.
的最小值是_____.
【答案】![]()
【解析】
如图,取AB的中点O,连接OC,OD,AE.想办法证明CE=CA,当CD是直径时![]() 的值最小.
的值最小.
如图,取AB的中点O,连接OC,OD,AE.
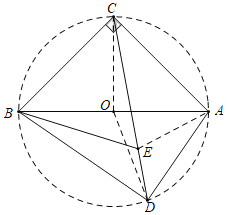
∵∠ACB=∠ADB=90°,OA=OB,
∴OC=OD=![]() AB,
AB,
∴A,C,B,D四点共圆,
∵CA=CB,
∴∠CBA=∠CBA=45°,
∴∠CDA=∠CBA=45°,∠CDB=∠CAB=45°,
∴∠CDB=∠CDA,
∵BE平分∠ABD,
∴AE平分∠BAD,
∴∠BAE=∠DAE,
∵∠CAE=∠CAB+∠BAE=45°+∠BAE,∠CEA=∠EDA+∠EAD=45°+∠DAE,
∴∠CAE=∠CEA,
∴CA=CE=定值,
∴当CD的值最大时,![]() 的值最小,
的值最小,
∴CD是直径时,![]() 的值最小,最小值=
的值最小,最小值=![]() =
=![]() ,
,
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
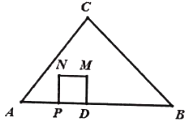
【题目】在![]() 中,
中,![]() ,
,![]() ,
,![]() ,点D在边AB上,且
,点D在边AB上,且![]() ,动点P从点A出发,以每秒1个单位长度的速度向终点B运动,以PD为边向上做正方形
,动点P从点A出发,以每秒1个单位长度的速度向终点B运动,以PD为边向上做正方形![]() ,设点P运动的时间为
,设点P运动的时间为![]() 秒,正方形
秒,正方形![]() 与
与![]() 重叠部分的面积为
重叠部分的面积为![]() .
.
(1)用含有![]() 的代数式表示线段
的代数式表示线段![]() 的长.
的长.
(2)当点![]() 落在
落在![]() 的边上时,求
的边上时,求![]() 的值.
的值.
(3)求![]() 与
与![]() 的函数关系式.
的函数关系式.
(4)当点P在线段AD上运动时,做点N关于CD的对称点![]() ,当
,当![]() 与
与![]() 的某一个顶点的连线平分
的某一个顶点的连线平分![]() 的面积时,求
的面积时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
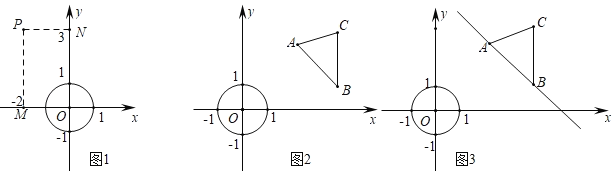
【题目】在平面直角坐标系xOy,对于点P(xp,yp)和图形G,设Q(xQ,yQ)是图形G上任意一点,|xp﹣xQ|的最小值叫点P和图形G的“水平距离”,|yp﹣yQ|的最小值叫点P和图形G的“竖直距离”,点P和图形G的“水平距离”与“竖直距离”的最大值叫做点P和图形G的“绝对距离”
例如:点P(﹣2,3)和半径为1的⊙O,因为⊙O上任一点Q(xQ,yQ)满足﹣1≤xQ≤1,﹣1≤yQ≤1,点P和⊙O的“水平距离”为|﹣2﹣xQ|的最小值,即|﹣2﹣(﹣1)|=1,点P和⊙O的“竖直距离”为|3﹣yQ|的最小值即|3﹣1|=2,因为2>1,所以点P和⊙O的“绝对距离”为2.
已知⊙O半径为1,A(2,![]() ),B(4,1),C(4,3)
),B(4,1),C(4,3)
(1)①直接写出点A和⊙O的“绝对距离”
②已知D是△ABC边上一个动点,当点D与⊙O的“绝对距离”为2时,写出一个满足条件的点D的坐标;
(2)已知E是△ABC边一个动点,直接写出点E与⊙O的“绝对距离”的最小值及相应的点E的坐标
(3)已知P是⊙O上一个动点,△ABC沿直线AB平移过程中,直接写出点P与△ABC的“绝对距离”的最小值及相应的点P和点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数![]() ,下列说法正确的个数是( )
,下列说法正确的个数是( )
①函数图象位于第一、三象限;②函数值 y 随 x 的增大而减小;③若 A(-1,![]() ),B(2,
),B(2,![]() ),C(1,
),C(1,![]() )是图象上三个点,则
)是图象上三个点,则![]() <
<![]() <
<![]() ;④P 为图象上任一点,过 P 作 PQ⊥y 轴于点 Q,则△OPQ 的面积是定值.
;④P 为图象上任一点,过 P 作 PQ⊥y 轴于点 Q,则△OPQ 的面积是定值.
A.1 个B.2 个C.3 个D.4 个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+(4a﹣1)x﹣4与x轴交于点A、B,与y轴交于点C,且OC=2OB,点D为线段OB上一动点(不与点B重合),过点D作矩形DEFH,点H、F在抛物线上,点E在x轴上.
(1)求抛物线的解析式;
(2)当矩形DEFH的周长最大时,求矩形DEFH的面积;
(3)在(2)的条件下,矩形DEFH不动,将抛物线沿着x轴向左平移m个单位,抛物线与矩形DEFH的边交于点M、N,连接M、N.若MN恰好平分矩形DEFH的面积,求m的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
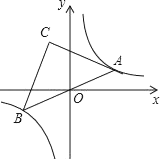
【题目】如图,点A是双曲线y=![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列赋予![]() 实际意义的叙述中不正确的是( )
实际意义的叙述中不正确的是( )
A. 若葡萄的价格是4元/千克,则![]() 表示买
表示买![]() 千克葡萄的金额
千克葡萄的金额
B. 若![]() 表示一个正方形的边长,则
表示一个正方形的边长,则![]() 表示这个正方形的周长
表示这个正方形的周长
C. 将一个小木块放在水平桌面上,若4表示小木块与桌面的接触面积,![]() 表示桌面受到的压强,则
表示桌面受到的压强,则![]() 表示小木块对桌面的压力
表示小木块对桌面的压力
D. 若4和![]() 分别表示一个两位数中的十位数字和个位数字,则
分别表示一个两位数中的十位数字和个位数字,则![]() 表示这个两位数
表示这个两位数
查看答案和解析>>
科目:初中数学 来源: 题型:
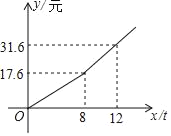
【题目】我国很多城市水资源缺乏,为了加强居民的节水意识,某市制定了每月用水8吨以内(包括8吨)和用水8吨以上两种收费标准(收费标准:每吨水的价格),某用户每月应交水费y(元)是用水量x(吨)的函数,其函数图象如图所示.
(1)求出自来水公司在这两个用水范围内的收费标准;
(2)若芳芳家6月份共交水费28.1元,请写出用水量超过8吨时应交水费y(元)与用水量x(吨)之间的函数关系,并求出芳芳家6月份的用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com