
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ����D�ڱ�AB�ϣ���
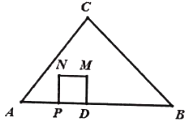
����D�ڱ�AB�ϣ���![]() ������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������
������P�ӵ�A��������ÿ��1����λ���ȵ��ٶ����յ�B�˶�����PDΪ��������������![]() �����P�˶���ʱ��Ϊ
�����P�˶���ʱ��Ϊ![]() �룬������
�룬������![]() ��
��![]() �ص����ֵ����Ϊ
�ص����ֵ����Ϊ![]() ��
��
��1���ú���![]() �Ĵ���ʽ��ʾ�߶�
�Ĵ���ʽ��ʾ�߶�![]() �ij���
�ij���
��2������![]() ����
����![]() �ı���ʱ����
�ı���ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��4������P���߶�AD���˶�ʱ������N����CD�ĶԳƵ�![]() ����
����![]() ��
��![]() ��ijһ�����������ƽ��
��ijһ�����������ƽ��![]() �����ʱ����
�����ʱ����![]() ��ֵ��
��ֵ��
���𰸡���1����0![]() t
t![]() 3ʱPD=3-t����3��t
3ʱPD=3-t����3��t![]() 7ʱ��PD=t-3����2��
7ʱ��PD=t-3����2��![]() ��
��![]() ����3��
����3��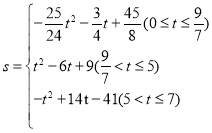 ����4��
����4��![]() ��
��![]() ��
��![]() ��
��
��������
��1����0��t��3ʱ��3��t��7ʱ���������ηֱ���⼴�ɣ�
��2����������������ͼ2�У�����N��AC��ʱ������ͼ3�У�����N��BC��ʱ������ƽ���߷��߶γɱ�������������⼴�ɣ�
��3�����������Σ�����ͼ4�У���0��t��![]() ʱ���ص������������EFPDM������ͼ5��6�У���
ʱ���ص������������EFPDM������ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN������ͼ7�У���5��t��7ʱ���ص������������EFPDM���ֱ���⼴�ɣ�
��t��5ʱ���ص�������������PDMN������ͼ7�У���5��t��7ʱ���ص������������EFPDM���ֱ���⼴�ɣ�
��4�����������λ���ͼ�Σ�����ƽ���߷��߶γɱ��������������̼��ɽ�����⣮
�⣺��1����ͼ1�У���CD���AB��D��
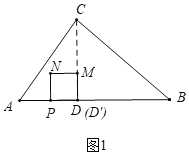
�ߡ�B��45�㣬BC��4![]() ��
��
��CD�䣽BD�䣽4��
�֡�CD���AB��![]() ��
��
����Rt��ACD����
AD�䣽![]() ��
��
��AD��3��
��AD��AD�䣬
��D����D�غϣ�
��0��t��3ʱ��PD��3��t��
��3��t��7ʱ��PD��t��3��
��2������ͼ2�У�����N��AC��ʱ��
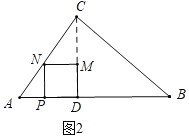
��MN��AD��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
����ͼ3�У�����N��BC��ʱ��
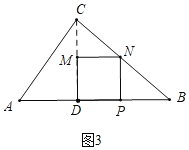
��MN��BD��
��![]() ��
��
��![]() ��
��
���t��5
��������������������t��ֵΪ![]() s��5s��
s��5s��
��3������ͼ4�У���0��t��![]() ʱ���ص������������EFPDM��
ʱ���ص������������EFPDM��
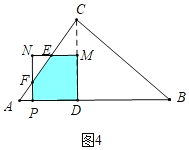
s��S������MDPN��S��NEF����3��t��2��![]()
����ͼ5��6�У���![]() ��t��5ʱ���ص�������������PDMN��s��t2��6t+9
��t��5ʱ���ص�������������PDMN��s��t2��6t+9
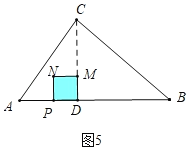
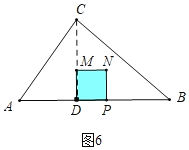
����ͼ7�У���5��t��7ʱ���ص������������EFPDM��s��S������MNPD��S��EFN����t��3��2��![]() [��t��3������7��t��]2����t2+14t��41��
[��t��3������7��t��]2����t2+14t��41��

����������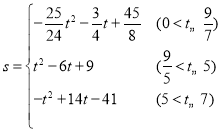 ��
��
��4����ͼ8�У�����N����������AE��ʱ����EK��BC��K��N��J��AB��J��
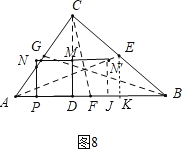
��JN���EK��
��![]() ��
��
����![]() ��
��
���t��1��
��ͼ9�У�����N����������BG��ʱ����GK��BC��K��N��J��/span>AB��J��
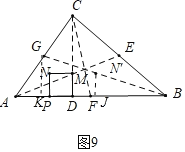
��N��J��GK��
��![]() ��
��
��![]() ��
��
���t��![]() ��
��
��ͼ10�У�����N����������CF��ʱ��
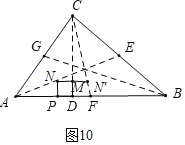
��MN���DF��
��![]() ��
��
��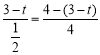 ��
��
���t��![]() ��
��
��������������������t��ֵΪ1s��![]() s��
s��![]() s��
s��


 ��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
��ʦ����ɳ���ʱͬ��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2019�괺���ڼ䣬�����п�չ��������������־Ըͬ����Ϊ�����ϵ��־Ը����.����ʦ�ͳ���ʦ�����μ�־Ը�����ʱ�������ĸ�־Ը�߹�����λ������ѡ��
��������ů�����λ��Ϊ���Ѽ�ͥ��ɨ������Ϊ���ض�ͯ�ṩѧҵ���������ֱ���![]() ��
��![]() ��ʾ��
��ʾ��
������ƽ�������λ��������ȫ��ʶ��������Ա�ܼ�����ά������.���ֱ���![]() ��
��![]() ��ʾ��
��ʾ��
��1������ʦ���ĸ���λ�����ѡȡһ��������ǡ��ѡ��������ů�����λ�ĸ����Ƕ��٣�
��2��������ʦ�ͳ���ʦ��������ĸ����λ��ѡһ��������������״ͼ���б����������ǡ�ö�ѡ��ͬһ����λ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ��
��![]() �ύ��
�ύ��![]() ���㣬ֱ��
���㣬ֱ��![]() ������
������![]() ���������ߵ���һ������Ϊ��
���������ߵ���һ������Ϊ��![]() ����
����![]() �ĺ�����Ϊ3���߶�
�ĺ�����Ϊ3���߶�![]() ���߶�
���߶�![]() ���ƶ���
���ƶ���![]() =1���ֱ����
=1���ֱ����![]() ��
��![]() ��Ĵ��ߣ�����������
��Ĵ��ߣ�����������![]() ,��ֱ����
,��ֱ����![]() .
.
(1)�������ߵĽ���ʽ;
(2)���ı���DEFGΪƽ���ı���ʱ�������ʱ��P��Q������;
(3)���߶�PQ���ƶ������У���D��E��F��GΪ������ı�������Ƿ������ֵ������������ֵ����û����˵������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ���ǰ���й���������ҵ��չѸ�٣������������г�������λ��ȫ��ҵǰ�У������Ǹ���ijý�巢����2012��2015�껥���������г���ģ��������ݣ����Ƶ�ͳ��ͼ����һ���֣�
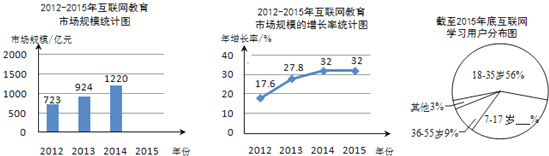
��1��2015�껥���������г���ģԼ�� ��Ԫ�������ȷ��1��Ԫ��������ȫ����ͳ��ͼ��
��2������2015��ף�Լ��5������ʹ�û���������ѧϰ��������ѧϰ�û�������ֲ���ͼ��ʾ�����㲹ȫ����ͳ��ͼ��������7��17��������� ������ͨ������������ѧϰ��
��3���������ϲ��ϣ�д�����˼�������ܻ��飨һ�����ɣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������״����������Ϯ�������人����������ij������ʿ���ι���N95����֧Ԯ�人����һ�λ���500000Ԫ���ڶ��λ���770000��������ͬ����N95���֣���֪�ڶ��ι���Ŀ��ֵĵ����ǵ�һ�ε�1.4�����ұȵ�һ�ζ����10000������ð�����ʿ��һ�ι������ֵĵ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
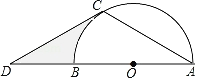
����Ŀ����ͼ��AB�ǡ�O��ֱ������D��AB�ӳ����ϵ�һ�㣬��C�ڡ�O�ϣ���AC��CD����ACD��120����
��1����֤��CD�ǡ�O�����ߣ�
��2������O�İ뾶Ϊ3����ͼ����Ӱ���ֵ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̶�м�2017��ɹ�����ȫ����������֮����������ȫ���������У�ijС��������Ӧ��������С���ڰ�װ�����������ܰ��ʾ�ƺ������䣬������2����ܰ��ʾ�ƺ�3�������乲��550Ԫ����������ĵ�������ܰ��ʾ�Ƶ��۵�3����
��1������ܰ��ʾ�ƺ�������ĵ��۸��Ƕ���Ԫ��
��2����С��������Ҫ����48�������䣬���������ܰ��ʾ�ƺ������乲100�����ҷ��ò�����10000Ԫ�������оٳ����й�������ָ�����ַ��������ʽ����٣������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����һ�㣬��ֱ��
����һ�㣬��ֱ��![]() ����
����![]() ����
����![]() ���ڵ�
���ڵ�![]() �������
�������![]() ����ô
����ô![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
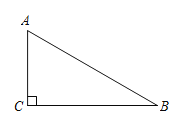
����Ŀ����ͼ1��ͼ2���ڡ�ABC�У�AB��13��BC��14��![]() .
.
̽������ͼ1��AH��BC�ڵ�H����AH��___��AC��___����ABC�����![]() ��___.
��___.
��չ����ͼ2����D��AC�ϣ������A��C�غϣ����ֱ����A��C��ֱ��BD�Ĵ��ߣ�����ΪE��F����BD��x��AE��m��CF��n��������D��A�غ�ʱ��������Ϊ![]() ��0��.
��0��.
��1���ú�x��m��n�Ĵ���ʽ��ʾ![]() ��
��![]() ��
��
��2����(m+n)��x�ĺ�����ϵʽ������(m+n)�����ֵ����Сֵ��
��3���Ը�����һ��xֵ����ʱֻ��ȷ��Ψһ�ĵ�D��ָ��������x��ȡֵ��Χ.
���֣�����ȷ��һ��ֱ�ߣ�ʹ��A��B��C���㵽����ֱ�ߵľ���֮����С������д�����̣�����д�������Сֵ.

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com