
科目:初中数学 来源: 题型:选择题
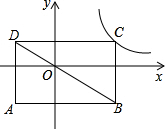 如图,在平面直角坐标系中,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在函数y=$\frac{k}{x}$(k>0,x>0)的图象上.若点A的坐标为(-3,-3),则k的值为( )
如图,在平面直角坐标系中,矩形ABCD的边平行于坐标轴,对角线BD经过坐标原点,点C在函数y=$\frac{k}{x}$(k>0,x>0)的图象上.若点A的坐标为(-3,-3),则k的值为( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
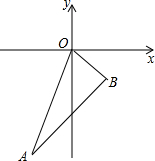 如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.
如图,直线OA的解析式为y=3x,点 A的横坐标是-1,OB=$\sqrt{2}$,OB与x轴所夹锐角是45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.
如图所示,已知数轴上两点A、B对应的数分别为-2、4,点P为数轴上一动点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
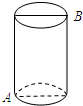 如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是13cm.
如图,圆柱体的高为12cm,底面周长为10cm,圆柱下底面A点除有一只蜘蛛,它想吃到上底面上与A点相对的B点处的苍蝇,需要爬行的最短路径是13cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x+4)2=7 | B. | (x+4)2=25 | C. | (x+4)2=-9 | D. | (x+8)2=7 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 38x-15=42x+5 | B. | 38x+15=42x-5 | C. | 42x+38x=15+5 | D. | 42x-38x=15-5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com