
在正方形ABCD中,点M是射线BC上一点,点N是CD延长线上一点,且BM=DN.直线BD与MN相交于E.
(1)如图1,当点M在BC上时,求证:BD-2DE= BM;
BM;
(2)如图2,当点M在BC延长线上时,BD、DE、BM之间满足的关系式是 ;(3)在(2)的条件下,连接BN交AD于点F,连接MF交BD于点G.若DE= ,
,
且AF:FD=1:2时,求线段DG的长.
 |
科目:初中数学 来源: 题型:
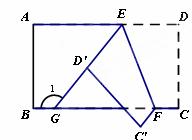
如图,将一张长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,ED′的延长线与BC相交于点G,若∠EFG=62°,则∠1=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率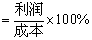 )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
演讲答辩环节,每位选手都从两个分别标有“A”、“B”内容的签中,随机抽取一个作为自 己的演讲内容,请你求出小明、小亮和小丽这三个选手中有两个抽中内容“A”,一个抽中内容“B”的概率.
己的演讲内容,请你求出小明、小亮和小丽这三个选手中有两个抽中内容“A”,一个抽中内容“B”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
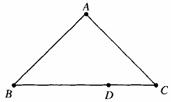
学校有一块菜地,如下图.现计划从点D表示的位置(BD∶DC=2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D是BC的中点的话,由此点D笔直地挖至点A就可以了.现在D不是BC的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图14,矩形ABCD和矩形AEFG关于点A中心对称,
(1)四边形BDEG是菱形吗?请说明理由;
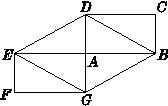
图14
(2)若矩形ABCD面积为2,求四边形BDEG的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com