
分析 首先由题意画出图形,易证得△OAB是等边三角形,又由正六边形的边心距为$\frac{\sqrt{3}}{2}$,利用三角函数的知识即可求得OA的长,即可得AB的长,继而求得它的周长.
解答 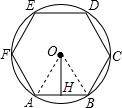 解:如图,连接OA,OB,
解:如图,连接OA,OB,
∵六边形ABCDEF是正六边形,
∴∠AOB=$\frac{1}{6}$×360°=60°,
∵OA=OB,
∴△OAB是等边三角形,
∴∠OAH=60°,
∵OH⊥AB,OH=$\frac{\sqrt{3}}{2}$,
∴OA=$\frac{OH}{sin60°}$=1,
∴AB=OA=1,
∴它的周长是:1×6=6.
故答案为:6.
点评 此题考查了圆的内接正多边形的性质、等边三角形的判定与性质、三角函数.此题难度不大,注意数形结合思想的应用.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=2,DF=3.求:
如图,在?ABCD中,AE⊥BC,AF⊥CD,∠EAF=60°,BE=2,DF=3.求:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
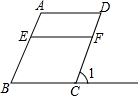 如图,E在AB上,F在DC上,G是BC延长线上的一点:
如图,E在AB上,F在DC上,G是BC延长线上的一点:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com