
分析 根据已知条件求得AC=3×4=12,BC=8,由M为AC的中点,得到AM=$\frac{1}{2}$AC=6,进一步得到BM=AM-AB=2,由于AB2=42=16,BM•BC=2×8=16,于是得到AB2=BM•BC,即可得到结论.
解答 解:线段AB是线段BM和BC的比例中项,
理由:∵AB=4,AC=3AB,
∴AC=3×4=12,BC=8,
∵M为AC的中点,
∴AM=$\frac{1}{2}$AC=6,
∴BM=AM-AB=2,
∵AB2=42=16,BM•BC=2×8=16,
∴AB2=BM•BC,
∴$\frac{AB}{BM}=\frac{BC}{AB}$,
∴线段AB是线段BM和BC的比例中项.
点评 本题考查了线段上两点间距离,比例线段,解题的关键是理解比例中项的含义.


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 总条数 | 50 | 45 | 60 | 48 | 10 | 30 | 42 | 38 | 15 | 10 |
| 标记数 | 2 | 1 | 3 | 2 | 0 | 1 | 1 | 2 | 0 | 1 |
| 总条数 | 53 | 36 | 27 | 34 | 43 | 26 | 18 | 22 | 25 | 47 |
| 标记数 | 2 | 1 | 2 | 1 | 2 | 1 | 1 | 2 | 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
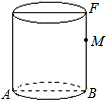 如图,已知圆柱体底面直径AB为2cm,高为4cm
如图,已知圆柱体底面直径AB为2cm,高为4cm 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com