
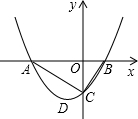
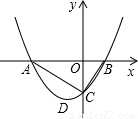
 物线的顶点,且∠ACB=90°,OA>OB.
物线的顶点,且∠ACB=90°,OA>OB.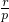 ,
,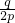 <0,p>0,
<0,p>0,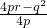 <r…①.
<r…①.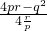 >r2…②,
>r2…②,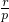 =1
=1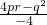 >1,即q2-4qr>4.
>1,即q2-4qr>4. (OA+OB)
(OA+OB) (-x1+x2)
(-x1+x2)
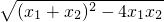

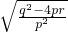 =
=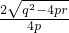
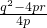 .
.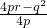 <r,在(1)中不难得出r=-p,再根据r2=-
<r,在(1)中不难得出r=-p,再根据r2=-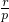 (即OC2=OA•OB,射影定理)即可求出所求的结论.
(即OC2=OA•OB,射影定理)即可求出所求的结论.

科目:初中数学 来源: 题型:
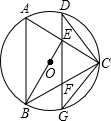 如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
如图,边长为4的等边三角形ABC内接于⊙O,直线EF经过边AC,BC的中点,交⊙O于D、G两点.
|
|
| p+pm |
| m |
查看答案和解析>>
科目:初中数学 来源: 题型:
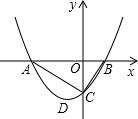 物线的顶点,且∠ACB=90°,OA>OB.
物线的顶点,且∠ACB=90°,OA>OB.查看答案和解析>>
科目:初中数学 来源:2003年全国中考数学试题汇编《二次函数》(03)(解析版) 题型:解答题
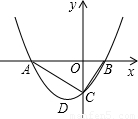
查看答案和解析>>
科目:初中数学 来源:2003年广东省肇庆市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com