
【题目】如图,已知AB⊥AD,AC⊥AE,AB=AD,AC=AE,BC分别交AD、DE于点G、F,AC与DE交于点H.求证: 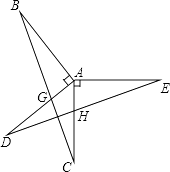
(1)△ABC≌△ADE;
(2)BC⊥DE.
【答案】
(1)证明:∵AB⊥AD,AC⊥AE,
∴∠DAB=∠CAE=90°,
∴∠DAB+∠DAC=∠CAE+∠DAC,
即∠BAC=∠DAE,
在△ABC和△ADE中,
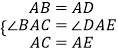
∴△ABC≌△ADE(SAS)
(2)证明:∵△ABC≌△ADE,
∴∠E=∠C,
∵∠E+∠AHE=90°,∠AHE=∠DHC,
∴∠C+∠DHC=90°,
∴BC⊥DE
【解析】(1)利用AB⊥AD,AC⊥AE,得出∠DAB=∠CAE,进一步得出∠BAC=∠DAE,再根据已知条件及全等的判定方法SAS即可证得△ABC≌△ADE;(2)由△ABC≌△ADE,得出∠E=∠C,利用∠E+∠AHE=90°,推出∠C+∠DHC=90°,结论成立.


科目:初中数学 来源: 题型:
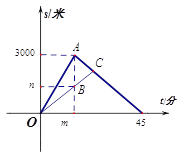
【题目】小明和爸爸周末到湿地公园进行锻炼,两人上午9:00从公园入口出发,沿相同路线匀速运动,小明15分钟后到达目的地,此时爸爸距出发地1200米,小明到达目的地后立即按原路匀速返回,与爸爸相遇后,和爸爸一起从原路返回出发地.小明、爸爸在锻炼过程中离出发地的路程与小明出发的时间的函数关系如图.
(1)图中![]() ,
, ![]() ;
;
(2)求小明和爸爸相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有理数a,b在数轴上的表示如图所示,则下列结论中: ①ab<0, ②![]() <0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
<0,③a+b<0,④a-b<0,⑤a<|b|,⑥-a>-b,正确的有( )
![]()
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某种礼炮的升空高度h(m)与飞行时间t(s)的关系式是h=﹣(t﹣4)2+20.若此礼炮在升空到最高处时引爆,则引爆需要的时间为( )
A.3sB.4sC.5sD.6s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形OABC的顶点A在y轴上,C在x轴上,双曲线y=![]() 与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )
与AB交于点D,与BC交于点E,DF⊥x轴于点F,EG⊥y轴于点G,交DF于点H.若矩形OGHF和矩形HDBE的面积分别是1和2,则k的值为( )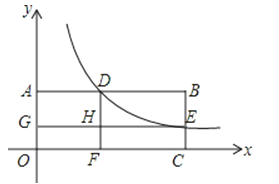
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某花园的护栏都是用直径![]() 的半圆形条钢组制而成,且每增加一个半圆形条钢,半圆护栏长度增加
的半圆形条钢组制而成,且每增加一个半圆形条钢,半圆护栏长度增加![]() ,(
,( ![]() )设半圆形条钢的总个数为
)设半圆形条钢的总个数为![]() (
(![]() 为正整数),护栏总长为
为正整数),护栏总长为![]() .
.
(![]() )当
)当![]() 时,用
时,用![]() 的代数式表示
的代数式表示![]() .
.
(![]() )若护栏总长度为
)若护栏总长度为![]() ,当
,当![]() 时,所用半圆形条钢的个数.
时,所用半圆形条钢的个数.
(![]() )若护栏的总长度不变,则当
)若护栏的总长度不变,则当![]() 时,用了
时,用了![]() 个半圆形条钢,当
个半圆形条钢,当![]() 时,用了
时,用了![]() 个半圆形条钢,请用含
个半圆形条钢,请用含![]() 的代数式表示
的代数式表示![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小丁在研究数学问题时遇到一个定义:对于排好顺序的三个数: ![]() ,称为数列
,称为数列![]() .计算
.计算![]() ,
, ![]() ,
, ![]() 将这三个数的最小值称为数列
将这三个数的最小值称为数列![]() 的价值.例如,对于数列2,﹣1,3,因为
的价值.例如,对于数列2,﹣1,3,因为![]() ,
, ![]() ,
, ![]() ,所以数列2,﹣1,3的价值为
,所以数列2,﹣1,3的价值为![]() .
.
小丁进一步发现:当改变这三个数的顺序时,所得到的数列都可以按照上述方法计算其相应的价值.如数列﹣1,2,3的价值为![]() ;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为
;数列3,﹣1,2的价值为1;….经过研究,小丁发现,对于“2,﹣1,3”这三个数,按照不同的排列顺序得到的不同数列中,价值的最小值为![]() .根据以上材料,回答下列问题:
.根据以上材料,回答下列问题:
(1)数列﹣4,﹣3,2的价值为 ;
(2)将“﹣4,﹣3,2”这三个数按照不同的顺序排列,可得到若干个数列,这些数列的价值的最小值为 ,取得价值最小值的数列为 (写出一个即可);
(3)将2,﹣9,a(a>1)这三个数按照不同的顺序排列,可得到若干个数列.若这些数列的价值的最小值为1,则a的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com