Question

【题目】已知：如图，反比例函数y= 的图象与一次函数y=x+b的图象交

于点A（1，4）、点B（-4，n）．

（1）求一次函数和反比例函数的解析式；

（2）求△OAB的面积；

（3）直接写出一次函数值大于反比例函数值的自变量x的取值范围．

Answer 1

【答案】（1）y=x+3；（2） ；（3）当x＞1或-4＜x＜0时，一次函数值大于反比例函数值．

【解析】试题分析：（1）把A的坐标代入反比例函数解析式求出A的坐标，把A的坐标代入一次函数解析式求出即可；
（2）求出直线AB与y轴的交点C的坐标，分别求出△ACO和△BOC的面积，然后相加即可；
（3）根据A、B的坐标结合图象即可得出答案．

试题解析：

（1）把A点（1，4）分别代入反比例函数y=k/x，一次函数y=x+b，得k=1×4，1+b=4，解得k=4，b=3，
∴反比例函数的解析式是y=4/x，一次函数解析式是y=x+3；
（2）如图，设直线y=x+3与y轴的交点为C，

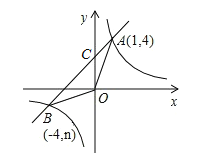
当x=-4时，y=-1，∴B（-4，-1），当x=0时，y=+3，∴C（0，3），

∴S△AOB=S△AOC+S△BOC=×3×4+×3×1=15/2

（3）∵B（-4，-1），A（1，4），∴根据图象可知：当x＞1或-4＜x＜0时，一次函数值大于反比例函数值．