已知⊙0中,半径r=5cm,AB,CD是两条平行弦,且AB=8cm,CD=6cm,则AC=________.

cm或5

cm或7

cm
分析:根据题意可以画出3个图形,分别过圆心作弦的垂线,得到直角三角形,运用勾股定理计算出AC的长.
解答:

解:如图1:分别过点O作OE⊥AB于E,OF⊥CD于F,CG⊥AB于G,
则EB=4,FD=3 连接OD,OB,
在Rt△OBE中,0E
2=OB
2-EB
2=25-16=9
∴OE=3.
在Rt△ODF中,OF
2=OD
2-DF
2=25-9=16.
∴OF=4.
EF=OF-OE=4-3=1=CG,
GE=CF=3,∴AG=1.
AC
2=AG
2+CG
2=1+1=2.
∴AC=

.
如图2:分别过点O作OE⊥AB于E,OF⊥CD于F,过C作CG⊥AB于G,

则EB=4,FD=3,连接OB,OD,
在Rt△OBE中,OE
2=0B
2-EB
2=25-16=9
∴OE=3.
在Rt△ODF中,OF
2=OD
2-FD
2=25-9=16
∴OF=4.
EF=OE+OF=3+4=7=CG.
AG=AF-GF=AF-CF=4-3=1.
AC
2=AG
2+CG
2=1+49=50.
∴AC=
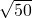
=5

.
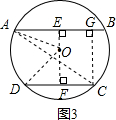
如图3:分别过O作OE⊥AB于E,OF⊥CD于F,过C作CG⊥AB于G,
则AE=4,DF=3,连接OA,OD,
在Rt△OAE中,OE
2=OA
2-AE
2=25-16=9
∴OE=3.
在Rt△ODF中,OF
2=OD
2-DF
2=25-9=16
∴OF=4.
EF=OE+OF=3+4=7=CG,
AG=AE+EG=4+3=7.
AC
2=AG
2+CG
2=47+49=98
∴AC=
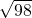
=7

.
故答案是:

或5

或7

.
点评:本题考查的是垂径定理,根据题意可以作出3个图形,在每个图形中由垂径定理分别过圆心作弦的垂线,构成直角三角形,然后在直角三角形中运用勾股定理计算可以求出AC的长.

 cm或5
cm或5 cm或7
cm或7 cm
cm 解:如图1:分别过点O作OE⊥AB于E,OF⊥CD于F,CG⊥AB于G,
解:如图1:分别过点O作OE⊥AB于E,OF⊥CD于F,CG⊥AB于G, .
.
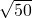 =5
=5 .
.
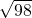 =7
=7 .
. 或5
或5 或7
或7 .
.

 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 (2012•宝安区二模)如图,已知⊙O中,半径OC⊥弦AB于点D,∠AOC=60°.
(2012•宝安区二模)如图,已知⊙O中,半径OC⊥弦AB于点D,∠AOC=60°.