
���� ��1���������ߵĽ���ʽ����������ߵĶԳ���Ϊx=4�����ݵ�A��y=x�Ͽ���õ�A������Ϊ��4��4��������4��4������0��0�����������ߵĽ���ʽ�����a��k��ֵ���Ӷ��õ������ߵĽ���ʽ��
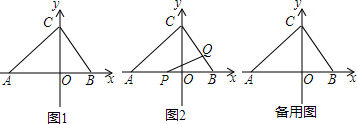
��2������P���߶�OA��ʱ����ͼ1��ʾ������P��PM��AD�ڵ�M���ڵ���������APM�У���������������Ǻ���ֵ�����PM=$\frac{\sqrt{2}}{2}$��4$\sqrt{2}$-2t����Ȼ�����������ε������ʽ�������S��t�Ĺ�ϵʽ����ͼ2��ʾ�������PM=$\frac{\sqrt{2}}{2}$��2t-4$\sqrt{2}$����Ȼ�����������ε������ʽ�������S��t�Ĺ�ϵʽ��
��3����ͼ3����֤����PAD�ա�ECD��AP=EC=$\sqrt{2}$����PA=AO-OP�ɵã�4$\sqrt{2}$-$\sqrt{2}t$=$\sqrt{2}$�����t=3����EF��x���ڵ�N����Rt��CEN�У���ECN=45�㣬CE=$\sqrt{2}$������CN=1���ʴ�ON=7����x=7���������ߵĽ���ʽ����õ�F�����ꣻ��ͼ4��ʾ����֤����PAD�ա�ECD���õ�AP=EC=$\sqrt{2}$������$\sqrt{2}t$-4$\sqrt{2}$=$\sqrt{2}$�����t=5��EF��x���ڵ�N����Rt��CEN�У���ECN=45�㣬CE=$\sqrt{2}$��CN=1���ʴ�ON=9����x=9���������ߵĽ���ʽ����õ�F�����꣮
��� �⣺��1����������y=a��x-4��2+k�Ķ���ΪA��
��A�ĺ�����Ϊ4��
�֡�ֱ��OA�Ľ���ʽΪy=x��
�൱x=4ʱ��y=4��
���A��������4��4����
����4��4������0��0������y=a��x-4��2+k�ã�a=-$\frac{1}{4}$��k=4��
�������ߵĽ���ʽΪy=-$\frac{1}{4}{x}^{2}+2x$��
��2������P���߶�OA��ʱ����ͼ1��ʾ������P��PM��AD�ڵ�M��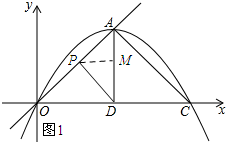
��ADΪ����������AOC�ױ�OC�ϵĸߣ�
���PAD=45��
��PM=APsin��PAD=$\frac{\sqrt{2}}{2}$��4$\sqrt{2}$-2t����
��${S}_{��APD}=\frac{1}{2}AD•PM$=$\frac{1}{2}��4��\frac{\sqrt{2}}{2}����4\sqrt{2}-\sqrt{2}t��$=8-2t��0��t��4����
����P���߶�OA���ӳ�����ʱ����ͼ2��ʾ������P��PM��AD�ڵ�M��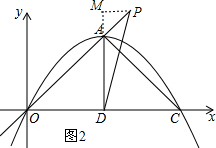
�ߡ�PAM=45�㣬
��PM=APsin��PAM=$\frac{\sqrt{2}}{2}��\sqrt{2}t-4\sqrt{2}��$��
��${S}_{��APD}=\frac{1}{2}AD•PM$=$\frac{1}{2}��4��\frac{\sqrt{2}}{2}��\sqrt{2}t-4\sqrt{2}��$=2t-8��t��4����
��S��t�ĺ�����ϵʽΪS=$\left\{\begin{array}{l}{8-2t��0��t��4��}\\{2t-8��t��4��}\end{array}\right.$��
��3����ͼ3��ʾ��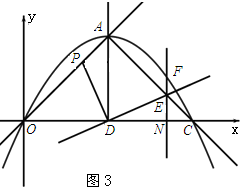
��PD��DE
���ADP=��EDC��
�ڡ�PAD�͡�ECD�У�$\left\{\begin{array}{l}{��ADP=��EDC}\\{AD=DC}\\{��PAD=��ECD=45��}\end{array}\right.$��
���PAD�ա�ECD��
��AP=EC=$\sqrt{2}$��
��4$\sqrt{2}$-$\sqrt{2}t$=$\sqrt{2}$��
��ã�t=3��
��EF��x���ڵ�N����Rt��CEN�У���ECN=45�㣬CE=$\sqrt{2}$��
��CN=CEcos��ECN=$\sqrt{2}��\frac{\sqrt{2}}{2}$=1
��ON=7��
��x=7���������ߵĽ���ʽ�ã�y=$-\frac{1}{4}��{7}^{2}+2��7=\frac{7}{4}$
���F��������7��$\frac{7}{4}$����
��ͼ4��ʾ��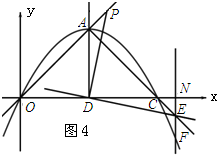
��PD��DE
���ADP=��EDC��
�ڡ�PAD�͡�ECD�У�$\left\{\begin{array}{l}{��ADP=��EDC}\\{AD=DC}\\{��PAD=��ECD=135��}\end{array}\right.$��
���PAD�ա�ECD��
��AP=EC=$\sqrt{2}$��
��$\sqrt{2}t$-4$\sqrt{2}$=$\sqrt{2}$��
��ã�t=5��
��EF��x���ڵ�N����Rt��CEN�У���ECN=45�㣬CE=$\sqrt{2}$��
��CN=CEcos��ECN=$\sqrt{2}��\frac{\sqrt{2}}{2}$=1
��ON=9��
��x=9���������ߵĽ���ʽ�ã�y=$-\frac{1}{4}��{9}^{2}+2��9$=$-\frac{9}{4}$
���F��������9��-$\frac{9}{4}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ����ȫ�������ε����ʺ��ж�������������Ǻ���ֵ�������ε������ʽ��֤�á�PAD�ա�ECD�ǽ���Ĺؼ���


 ��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
��Ǭ����������ҵ���ּ����ӱ����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ���ı���ABEG��GEFH��HFCD���DZ߳�Ϊa�������Σ���AEF���CEA������Ϊʲô��
��ͼ���ı���ABEG��GEFH��HFCD���DZ߳�Ϊa�������Σ���AEF���CEA������Ϊʲô���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
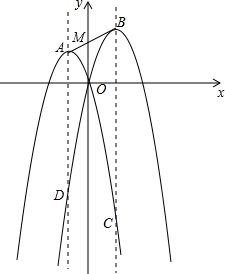 ��ͼ��������C1��y=-��x+m��2+m2��m��0���Ķ���ΪA��������C2��y=-��x-n��2+n2��n��m���Ķ���ΪB��������C2�ĶԳ�����������C1�ཻ�ڵ�C��������C1�ĶԳ�����������C2�ཻ�ڵ�D��
��ͼ��������C1��y=-��x+m��2+m2��m��0���Ķ���ΪA��������C2��y=-��x-n��2+n2��n��m���Ķ���ΪB��������C2�ĶԳ�����������C1�ཻ�ڵ�C��������C1�ĶԳ�����������C2�ཻ�ڵ�D���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
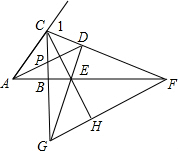 ��ͼ��Rt��ABC�У���CBA=90�㣬��CAB�Ľ�ƽ����AP�͡�ACB�����ƽ����CF�ཻ�ڵ�D��AD��CB��P��CF��AB���ӳ�����F����D��DE��CF��CB���ӳ����ڵ�G����AB���ӳ����ڵ�E������CE���ӳ��߽�FG�ڵ�H�������н��ۣ��١�CDA=45�㣻��AF-CG=CA����DE=DC����FH=CD+GH����CF=2CD+EG��������ȷ���Т٢ڢۢݣ�
��ͼ��Rt��ABC�У���CBA=90�㣬��CAB�Ľ�ƽ����AP�͡�ACB�����ƽ����CF�ཻ�ڵ�D��AD��CB��P��CF��AB���ӳ�����F����D��DE��CF��CB���ӳ����ڵ�G����AB���ӳ����ڵ�E������CE���ӳ��߽�FG�ڵ�H�������н��ۣ��١�CDA=45�㣻��AF-CG=CA����DE=DC����FH=CD+GH����CF=2CD+EG��������ȷ���Т٢ڢۢݣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com