
五边形ABCDE中,∠EAB=∠ABC=∠BCD=90°,AB=BC,且满足以点B为圆心,AB长为半径的圆弧AC与边DE相切于点F,连接BE,BD.
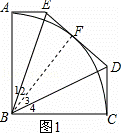
(1)如图1,求∠EBD的度数;
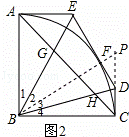
(2)如图2,连接AC,分别与BE,BD相交于点G,H,若AB=1,∠DBC=15°,求AG•HC的值.
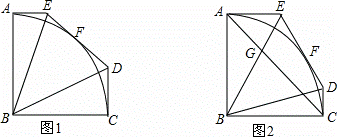
解:(1)如图1,连接BF,
∵DE与⊙B相切于点F,
∴BF⊥DE,
在Rt△BAE与Rt△BEF中,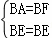 ,
,
∴Rt△BAE≌Rt△BEF,
∴∠1=∠2,
同理∠3=∠4,
∵∠ABC=90°,
∴∠2+∠3=45°,
即∠EBD=45°;
(2)如图2,连接BF并延长交CD的延长线于P,
∵∠4=15°,
由(1)知,∠3=∠4=15°,
∴∠1=∠2=30°,∠PBC=30°,
∵∠EAB=∠PCB=90°,AB=1,
∴AE=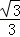 ,BE=
,BE=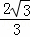 ,
,
在△ABE与△PBC中,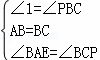 ,
,
∴△ABE≌△PBC,
∴PB=BE=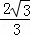 ,
,
∴PF=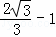 ,
,
∵∠P=60°,
∴DF=2﹣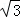 ,
,
∴CD=DF=2﹣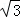 ,
,
∵∠EAG=∠DCH=45°,
∠AGE=∠BDC=75°,
∴△AEG∽△CHD,
∴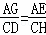 ,
,
∴AG•CH=CD•AE,
∴AG•CH=CD•AE=(2﹣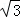 )•
)•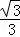 =
=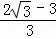 .
.


科目:初中数学 来源:2014-2015学年江苏省联盟九年级下学期第一次月考数学试卷(解析版) 题型:解答题
(10分)有一个不透明口袋,装有分别标有数字1,2,3,4的4个小球(小球除数字不同外,其余
都相同),另有3张背面完全一样、正面分别写有数字1,2,3的卡片.小敏从口袋中任意摸出一个小球,小
颖从这3张背面朝上的卡片中任意摸出一张,然后计算摸出的小球和卡片上的两个数的积.
(1)请你用列表或画树状图的方法,求摸出的这两个数的积为6的概率;
(2)小敏和小颖做游戏,她们约定:若这两个数的积为奇数,小敏赢;否则,小颖赢.你认为该游戏公平吗?为什么?如果不公平,请你修改游戏规则,使游戏公平.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级4月阶段检测数学试卷(解析版) 题型:选择题
对于每个正整数n,设f(n)表示n(n+1)的末位数字.例如:f(1)=2(1×2的末位数字),f(2)=6(2×3的末位数字),f(3)=2(3×4的末位数字),……则f(1)+f(2)+f(3)+…+f(2012)的值为 ( )
A.6 B.4022 C.4028 D.6708
查看答案和解析>>
科目:初中数学 来源: 题型:
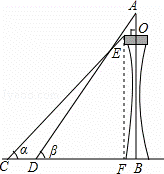
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据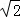 ≈1.4,
≈1.4,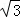 ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知关于x的一元二次方程3x2+4x﹣5=0,下列说法不正确的是( )
A.方程有两个相等的实数根 B.方程有两个不相等的实数根
C.没有实数根 D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
a是不为1的数,我们把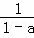 称为a的差倒数,如:2的差倒数为
称为a的差倒数,如:2的差倒数为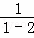 =﹣1;﹣1的差倒数是
=﹣1;﹣1的差倒数是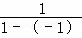 =
=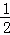 ;已知a1=3,a2是a1的差倒数,a3是a2的差倒数.a4是a3差倒数,…依此类推,则a2015=
;已知a1=3,a2是a1的差倒数,a3是a2的差倒数.a4是a3差倒数,…依此类推,则a2015=
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com