3

-5
分析:由EF∥BC,可得△AEF∽△ABC,根据相似三角形的面积比等于相似比的平方,可得
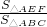
=(

)
2,然后设
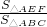
=(

)
2=x
2,即可得EF:BC=x,由同高三角形的面积比等于对应底的比,即可得S
△EFC:S
△EBC=EF:BC=x,继而可求得S
△ABC=S
△EBC+S
△AEF+S
△EFC=(3+x)S
△EBC,即可得方程
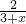
=x
2,解此方程即可求得x的值,继而求得答案.
解答:∵EF∥BC,
∴△AEF∽△ABC,
∴
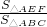
=(

)
2,
设
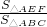
=(

)
2=x
2,
∴EF:BC=x,
∴S
△EFC:S
△EBC=EF:BC=x,
∴S
△EFC=xS
△EBC,
∵S
△AEF=2S
△EBC,
∴S
△ABC=S
△EBC+S
△AEF+S
△EFC=(3+x)S
△EBC,
∴
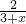
=x
2,
∴x
3+3x
2-2=0,
即x
3+x
2+2x
2-2=0,
∴x
2(x+1)+2(x+1)(x-1)=0
∴(x+1)(x
2+2x-2)=0,
∴x+1=0或x
2+2x-2=0,
解得:x=-1(舍去)或x=

+1(舍去)或x=

-1,
∴S
△AEF=x
2•S
△ABC=4-2

,
∴S
△EFC=xS
△EBC=

S
△AEF=

×(4-2

)=3

-5.
故答案为:3

-5.
点评:此题考查了相似三角形的判定与性质.此题难度较大,注意掌握数形结合思想与方程思想的应用是解此题的关键.

 如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC,若△ABC的面积为1,S△AEF=2S△EBC,则S△CEF为________.
如图,在△ABC中,点E,F分别在边AB,AC上,EF∥BC,若△ABC的面积为1,S△AEF=2S△EBC,则S△CEF为________. -5
-5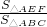 =(
=( )2,然后设
)2,然后设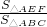 =(
=( )2=x2,即可得EF:BC=x,由同高三角形的面积比等于对应底的比,即可得S△EFC:S△EBC=EF:BC=x,继而可求得S△ABC=S△EBC+S△AEF+S△EFC=(3+x)S△EBC,即可得方程
)2=x2,即可得EF:BC=x,由同高三角形的面积比等于对应底的比,即可得S△EFC:S△EBC=EF:BC=x,继而可求得S△ABC=S△EBC+S△AEF+S△EFC=(3+x)S△EBC,即可得方程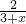 =x2,解此方程即可求得x的值,继而求得答案.
=x2,解此方程即可求得x的值,继而求得答案.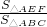 =(
=( )2,
)2,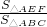 =(
=( )2=x2,
)2=x2,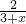 =x2,
=x2, +1(舍去)或x=
+1(舍去)或x= -1,
-1, ,
, S△AEF=
S△AEF= ×(4-2
×(4-2 )=3
)=3 -5.
-5. -5.
-5.

 如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为
如图,在△ABC中,∠ACB=90°,AC=BC=1,取斜边的中点,向斜边作垂线,画出一个新的等腰三角形,如此继续下去,直到所画出的直角三角形的斜边与△ABC的BC重叠,这时这个三角形的斜边为