
【题目】已知抛物线![]() 与x轴交于A、B两点.
与x轴交于A、B两点.
(1)求证:抛物线的对称轴在y轴的左侧;
(2)若![]() (O为坐标原点),求抛物线的解析式;
(O为坐标原点),求抛物线的解析式;
(3)设抛物线与y轴交于点C,若△ABC是直角三角形.求△ABC的面积.
【答案】(1)见解析(2)y=x2+2x﹣3;(3)![]()
【解析】
试题分析:(1)证明抛物线的对称轴<0即可证明抛物线的对称轴在y轴的左侧;
(2)根据题中已知条件求出m的值,进而求得抛物线的解析式;
(3)先设出C点坐标,根据的x1与x2关系求出m值,进而可求得△ABC的面积.
(1)证明:∵m>0,
∴x=﹣![]() =﹣
=﹣![]() <0,
<0,
∴抛物线的对称轴在y轴的左侧;
(2)解:设抛物线与x轴交点为A(x1,0),B(x2,0),
则x1+x2=﹣m<0,x1x2=﹣![]() m2<0,
m2<0,
∴x1与x2异号,
又∵![]() =
=![]() >0,
>0,
∴OA>OB,
由(1)知:抛物线的对称轴在y轴的左侧,
∴x1<0,x2>0,
∴OA=|x1|=﹣x1,
OB=x2,
代入![]() 得:
得:![]() =
=![]() ,
,
![]() =
=![]() ,
,
从而 ,
,
解得m=2,
经检验m=2是原方程的根,
∴抛物线的解析式为y=x2+2x﹣3;
(3)解:当x=0时,y=﹣![]() m2
m2
∴点C(0,﹣![]() m2),
m2),
∵△ABC是直角三角形,
∴AB2=AC2+BC2,
∴(x1﹣x2)2=x12+(﹣![]() m2)2+x22+(﹣
m2)2+x22+(﹣![]() m2)2
m2)2
∴﹣2x1x2=![]() m4
m4
∴﹣2(﹣![]() m2)=
m2)=![]() m4,
m4,
解得m=![]() ,
,
∴S△ABC=![]() ×ABOC=
×ABOC=![]() |x1﹣x2|
|x1﹣x2|![]() =
=![]() ×2m×
×2m×![]() m2=
m2=![]() .
.


科目:初中数学 来源: 题型:
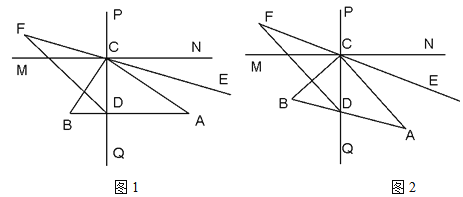
【题目】已知:如图,直线![]() ⊥
⊥![]() 于点
于点![]() ,△
,△![]() 是直角三角形,且∠
是直角三角形,且∠![]() =90°,斜边
=90°,斜边![]() 交直线
交直线![]() 于点
于点![]() ,
,![]() 平分∠
平分∠![]() ,∠
,∠![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() ,∠
,∠![]() =36°.
=36°.
(1)如图1,当![]() ∥
∥![]() 时,求∠
时,求∠![]() 的度数.
的度数.
(2)如图2,当△![]() 绕
绕![]() 点旋转一定的角度(即
点旋转一定的角度(即![]() 与
与![]() 不平行),其他条件不变,问∠
不平行),其他条件不变,问∠![]() 的度数是否发生改变?请说明理由.
的度数是否发生改变?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据下列证明过程填空:
已知:如 图,AD⊥BC于点D,EF⊥BC于点F,交AB于点G,交CA的延长线于点E,∠1=∠2.
求证:AD平分∠BAC,填写证明中的空白.
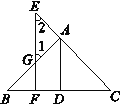
证明:
∵AD⊥BC,EF⊥BC (已知),
∴EF∥AD ( ),
∴_______ _ = ________ ( 两直线平行,内错角相等 ),
________ =∠CAD ( ____________ ).
∵________ (已知),
∴________ ,即AD平分∠BAC ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
问题探究:(1)已知:如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE丄DH于点O,求证:AE=DH
类比探究:(2)已知:如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,则线段EF与HG有什么数量关系,并说明理由;
拓展应用:(3)已知:如图3,在(2)问条件下,若HF∥GE,BE=EC=2,EO=2FO,求HG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某单位要招聘1名英语翻译,张明参加招聘考试的成绩如表所示,若把听、说、读、写的成绩按30%,30%,20%,20%计算成绩,则张明的成绩为_____.
听 | 说 | 读 | 写 | |
张明 | 90 | 80 | 83 | 82 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断中正确的是( )
A. 四边相等的四边形是正方形 B. 四角相等的四边形是正方形
C. 对角线相互垂直平分的平行四边形是正方形 D. 对角线互相垂直平分且相等的四边形是正方形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com