Question

【题目】

问题探究：（1）已知：如图1，在正方形ABCD中，点E，H分别在BC，AB上，若AE丄DH于点O，求证：AE=DH

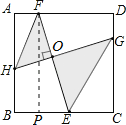
类比探究：（2）已知：如图2，在正方形ABCD中，点H，E，G，F分别在AB，BC，CD，DA上，若EF⊥HG于点O，则线段EF与HG有什么数量关系，并说明理由；

拓展应用：（3）已知：如图3，在（2）问条件下，若HF∥GE，BE=EC=2，EO=2FO，求HG的长．

Answer 1

【答案】（1）见解析；（2）EF=GH，理由见解析；（3）GH=．

【解析】

试题分析：（1）由正方形的性质得AB=DA，∠ABE=90°=∠DAH．所以∠HAO+∠OAD=90°，又知∠ADO+∠OAD=90°，所以∠HAO=∠ADO，于是△ABE≌△DAH，可得AE=DH；

（2）EF=GH．将FE平移到AM处，则AM∥EF，AM=EF，将GH平移到DN处，则DN∥GH，DN=GH．根据（1）的结论得AM=DN，所以EF=GH；

（3）易得△AHF∽△CGE，所以，由EC=2得AF=1，过F作FP⊥BC于P，根据勾股定理得EF=，根据（2）①知EF=GH，即可得到结论．

解：（1）∵四边形ABCD是正方形，

∴AB=DA，∠ABE=90°=∠DAH．

∴∠HAO+∠OAD=90°．

∵AE⊥DH，

∴∠ADO+∠OAD=90°．

∴∠HAO=∠ADO．

∴△ABE≌△DAH（ASA），

∴AE=DH．

（2）EF=GH．

将FE平移到AM处，则AM∥EF，AM=EF．

将GH平移到DN处，则DN∥GH，DN=GH．

∵EF⊥GH，

∴AM⊥DN，

根据（1）的结论得AM=DN，所以EF=GH；

（3）∵四边形ABCD是正方形，

∴AB∥CD

∴∠AHO=∠CGO

∵FH∥EG

∴∠FHO=∠EGO

∴∠AHF=∠CGE

∴△AHF∽△CGE

∴，

∵EC=2，

∴AF=1，

过F作FP⊥BC于P，

根据勾股定理得EF==

根据（2）知EF=GH，

∴GH=．