
����Ŀ����ͼ������ABCD�У�AB=6cm��BC=8cm��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ������������У��ٶȾ�Ϊ2cm/s���˶�ʱ��Ϊt��0��t��5���룮
��1����G��H�ֱ���AB��DC���е㣬��t��2.5s����֤����E��G��F��HΪ������ı���ʼ����ƽ���ı��Σ�
��2���ڣ�1���������£���tΪ��ֵʱ����E��G��F��HΪ������ı����Ǿ��Σ�
��3����G��H�ֱ�������A-B-C��C-D-A�ϵĶ��㣬�ֱ��A��C��ʼ����E��F��ͬ���ٶ�ͬʱ��������tΪ��ֵʱ����E��G��F��HΪ������ı��������Σ���ֱ��д��t��ֵ��
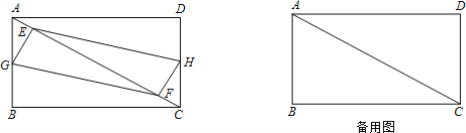
���𰸡���1��֤������������2����tΪ4.5���0.5��ʱ���ı���EGFH�Ǿ��Σ���3��tΪ![]() ��ʱ���ı���EGFH�����Σ�
��ʱ���ı���EGFH�����Σ�
��������
��1�����ݹ��ɶ������AC��֤����AFG�ա�CEH������ȫ�������ε����ʵõ�GF=HE�������ڴ�����ȵ�GF��HE������ƽ���ı��ε��ж��ɵý��ۣ�
��2����ͼ1������GH����AC-AE-CF=8��AE+CF-AC=8����������з��̼��㼴�ɣ�
��3������AG��CH���ж��ı���AGCH�����Σ��õ�AG=CG�����ݹ��ɶ������BG���õ�AB+BG�ij�������������
�⣺��1�����ı���ABCD�Ǿ��Σ�
��AB=CD��AB��CD��AD��BC����B=90����
���BAC=��DCA��
��AB=6cm��BC=8cm��
��AC=10cm��
��G��H�ֱ���AB��DC���е㣬
��AG=![]() AB��CH=
AB��CH=![]() CD��
CD��
��AG=CH��
��E��F�ǶԽ���AC�ϵ��������㣬�ֱ��A��Cͬʱ������������У��ٶȾ�Ϊ2cm/s��
��AE=CF��
��AF=CE��
���AGF�ա�CHE��SAS����
��GF=HE����AFG=��CEH��
��GF��HE��
����E��G��F��HΪ������ı���ʼ����ƽ���ı��Σ�
��2����ͼ1������GH���ɣ�1����֪�ı���EGFH��ƽ���ı��Σ�
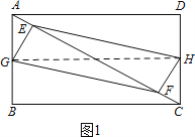
��G��H�ֱ���AB��DC���е㣬
��GH=BC=8cm��
�൱EF=GH=8cmʱ���ı���EGFH�Ǿ��Σ������������
����AE=CF=2t����EF=10-4t=8����ã�t=0.5��
����AE=CF=2t����EF=2t+2t-10=8����ã�t=4.5��
����tΪ4.5���0.5��ʱ���ı���EGFH�Ǿ��Σ�
��3����ͼ2������AG��CH��
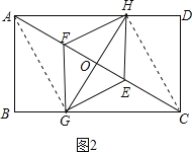
���ı���GEHF�����Σ�
��GH��EF��OG=OH��OE=OF��
��AF=CE
��OA=OC��
���ı���AGCH�����Σ�
��AG=CG��
��AG=CG=x����BG=8-x��
�ɹ��ɶ����ã�AB2+BG2=AG2��
��62+��8-x��2=x2����ã�x=![]() ��
��
��BG=8-![]() =
=![]() ��
��
��AB+BG=6+![]() =
=![]() ��
��
t=![]() ��2=
��2=![]() ��
��
��tΪ![]() ��ʱ���ı���EGFH�����Σ�
��ʱ���ı���EGFH�����Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���![]() ��Ϊ
��Ϊ![]() �Ḻ������һ�㣬��
�Ḻ������һ�㣬��![]() Ϊ
Ϊ![]() ����������һ�㣬����
����������һ�㣬����![]() ���㷽��
���㷽��![]() ��
��
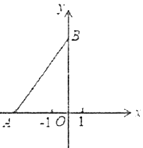
��1�����![]() ��
��![]() �����ꣻ
�����ꣻ
��2����![]() Ϊ
Ϊ![]() �Ḻ������һ�㣬��
�Ḻ������һ�㣬��![]() �����Ϊ
�����Ϊ![]() �����
�����![]() �����ꣻ
�����ꣻ
��3����![]() ���Ƿ����һ��
���Ƿ����һ��![]() ��ʹ
��ʹ![]() ���������
���������![]() �������һ�룬�����ڣ������Ӧ��
�������һ�룬�����ڣ������Ӧ��![]() ������꣬�������ڣ���˵�����ɣ�
������꣬�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=AD=6��AB��BC��AD��CD����BAD=60������M��N�ֱ���AB��AD���ϣ���AM��MB=AN��ND=1��2����tan��MCN=

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У�O��BC���е㣬D�ǡ�BACƽ�����ϵ�һ�㣬��DO��BC������D�ֱ���DM��AB��M��DN��AC��N����֤��BM��CN��
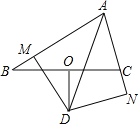
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ���е�A(1��0)����A��һ����������![]() ���ڶ��ε�
���ڶ��ε�![]() ��������
��������![]() �����ε�
�����ε�![]() ��������
��������![]() �����Ĵε�
�����Ĵε�![]() ��������
��������![]() ���������˹���������ȥ�����
���������˹���������ȥ�����![]() ���
���![]() ֮��ľ����ǣ� ��
֮��ľ����ǣ� ��

A. 2017B. 2018C. 2019D. 2020
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���»��̳�����ij�ֱ��䣬ÿ̨����Ϊ2500Ԫ�����ۼ�Ϊ2900Ԫ��ƽ��ÿ�����۳�8̨�����鷢�֣������ۼ�ÿ����50Ԫ��ƽ��ÿ����ܶ��۳�4̨���̳�Ҫ��ʹ���ֱ������������ƽ��ÿ��ﵽ5000Ԫ��ÿ̨����Ӧ�ý��۶���Ԫ������ÿ̨���併��xԪ������������з��̣�������
A. (2900-x)(8+4��![]() )=5000 B. (400-x)(8+4��
)=5000 B. (400-x)(8+4��![]() )=5000
)=5000
C. 4(2900-x)(8+![]() )=5000 D. 4(400-x)(8+
)=5000 D. 4(400-x)(8+![]() )=5000
)=5000
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=AC=1����A=45�����߳�Ϊ1�������ε�һ������D�ڱ�AC�ϣ����ABC�����߷ֱ��ڵ�E��F��DE��AB����������ƽ�ƣ�ʹ��D������AC�ϣ�D����A�غϣ�����AF=x�����������ABC�ص����ֵ����Ϊy��
(1)��y��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ��
(2)xΪ��ֵʱy��ֵ���
(3)x���ĸ���Χȡֵʱy��ֵ��x���������С��
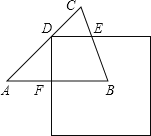
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=![]() AB����֤����B=30�㣮
AB����֤����B=30�㣮
������������֤����
֤������ͼ����Rt��ABC��б���ϵ�����CD��
�� CD=![]() AB=AD ���� ������
AB=AD ���� ������
��AC=![]() AB��
AB��
��AC=CD=AD ����ACD�ǵȱ������Σ�
���A=�� ���㣮
���B=90�㩁��A=30�㣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���BAC=90����AC=2AB����D��AC���е㣮��һ�����Ϊ45����ֱ�����ǰ���ͼ���ã�ʹ���ǰ�б�ߵ������˵�ֱ���A��D�غϣ�����BE��EC��
 �Բ����߶�BE��EC��������λ�ù�ϵ����֤����IJ��룮
�Բ����߶�BE��EC��������λ�ù�ϵ����֤����IJ��룮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com