【题目】如图，在Rt△ABC中，∠C=90°，AC=
AB．求证：∠B=30°．
请填空完成下列证明．
证明：如图，作Rt△ABC的斜边上的中线CD，
则 CD=AB=AD （ ）．
∵AC=AB，
∴AC=CD=AD 即△ACD是等边三角形．
∴∠A= °．
∴∠B=90°﹣∠A=30°．
科目：初中数学 来源： 题型：
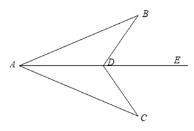
【题目】如图，已知AE平分∠BAC,点D是AE上一点，连接BD,CD.请你添加一个适当的条件，使△ABD≌△ACD.添加的条件是：____.（写出一个即可）
查看答案和解析>>
科目：初中数学 来源： 题型：
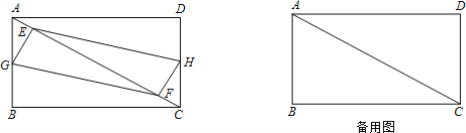
【题目】如图，矩形ABCD中，AB=6cm，BC=8cm，E、F是对角线AC上的两个动点，分别从A、C同时出发，相向而行，速度均为2cm/s，运动时间为t（0≤t≤5）秒．
（1）若G、H分别是AB、DC的中点，且t≠2.5s，求证：以E、G、F、H为顶点的四边形始终是平行四边形；
（2）在（1）的条件下，当t为何值时？以E、G、F、H为顶点的四边形是矩形；
（3）若G、H分别是折线A-B-C，C-D-A上的动点，分别从A、C开始，与E．F相同的速度同时出发，当t为何值时，以E、G、F、H为顶点的四边形是菱形，请直接写出t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商场购进一种单价为40元的足球，如果以单价50元售出，那么每月可售出500个，根据销售经验，销售单价每提高1元，销售量相应减少10个.
（1）设销售单价提高x元(x为正整数)，写出每月销售量y（个）与x（元）之间的函数关系式；
（2）假设这种篮足球每月的销售利润为w元，试写出w与x之间的函数关系式，并通过配方讨论，当销售单价定为多少元时，每月销售这种足球的利润最大，最大利润为多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，对称轴为直线
的抛物线
与x轴相交于A、B两点，其中A点的坐标为（－3，0）。
（1）求点B的坐标；
（2）已知
，C为抛物线与y轴的交点。
①若点P在抛物线上，且
，求点P的坐标；
②设点Q是线段AC上的动点，作QD⊥x轴交抛物线于点D，求线段QD长度的最大值。
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】“早黑宝”是我省农科院研制的优质新品种，在我省被广泛种植．清徐县某葡萄种植基地2016年种植“早黑宝”100亩，到2018年“早黑宝”的种植面积达到225亩．
(1)求该基地这两年“早黑宝”种植面积的平均增长率；
(2)市场调查发现，当“早黑宝”售价为20元/千克时，每天能售出200千克，售价每降低1元，每天可多售出50千克，为了推广宣传，基地决定降价促销，已知该基地“早黑宝”的平均成本价为12元/千克，若使销售“早黑宝”每天获利1800元，则售价应降低多少元？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】综合与实践
问题情境：正方形折叠中的数学
已知正方形纸片ABCD中，AB=4，点E是AB边上的一点，点G是CE的中点，将正方形纸片沿CE所在直线折叠，点B的对应点为点B′．
(1)如图1，当∠BCE=30°时，连接BG，B′G，求证：四边形BEB′G是菱形；
深入探究：
(2)在CD边上取点F，使DF=BE，点H是AF的中点，再将正方形纸片ABCD沿AF所在直线折叠，点D的对应点为D′，顺次连接B′，G，D′，H，B'，得到四边形B′GD′H．
请你从A，B两题中任选一题作答，我选择 题．
A题：如图2，当点B'，D′均落在对角线AC上时，
①判断B′G与D′H的数量关系与位置关系，并说明理由；
②直写出此时点H，G之间的距离．
B题：如图3，点M是AB的中点，MN∥BC交CD于点N，当点B'，D′均落在MN上时，
①判断B′G与D′H的数量关系与位置关系，并说明理由；
②直接写出此时点H，G之间的距离．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】联想三角形内心的概念，我们可引入如下概念．
定义：到三角形的两边距离相等的点，叫做此三角形的准内心．
举例：如图1，若PD=PE，则点P为△ABC的准内心．
应用：如图2，BF为等边三角形的角平分线，准内心P在BF上，且PF=
BP，求证：点P是△ABC的内心．
探究：已知△ABC为直角三角形，∠C=90°，准内心P在AC上，若PC=AP，求∠A的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
