
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
【答案】解:(1)∵A、B两点关于对称轴![]() 对称 ,且A点的坐标为(-3,0),
对称 ,且A点的坐标为(-3,0),
∴点B的坐标为(1,0)。
(2)①∵抛物线![]() ,对称轴为
,对称轴为![]() ,经过点A(-3,0),
,经过点A(-3,0),
∴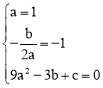 ,解得
,解得![]() 。
。
∴抛物线的解析式为![]() 。
。
∴B点的坐标为(0,-3)。∴OB=1,OC=3。∴![]() 。
。
设点P的坐标为![]() ,则
,则![]() 。
。
∵![]() ,∴
,∴![]() ,解得
,解得![]() 。
。
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
∴点P的坐标为(2,5)或(-2,-3)。
②设直线AC的解析式为![]() ,将点A,C的坐标代入,得:
,将点A,C的坐标代入,得:
![]() ,解得:
,解得:![]() 。
。
∴直线AC的解析式为![]() 。
。
∵点Q在线段AC上,∴设点Q的坐标为![]() 。
。
又∵QD⊥x轴交抛物线于点D,∴点D的坐标为![]() 。
。
∴![]() 。
。
∵![]() ,∴线段QD长度的最大值为
,∴线段QD长度的最大值为![]() 。
。
【解析】(1)由抛物线的对称性直接得点B的坐标。
(2)①用待定系数法求出抛物线的解析式,从而可得点C的坐标,得到![]() ,设出点P 的坐标,根据
,设出点P 的坐标,根据![]() 列式求解即可求得点P的坐标。
列式求解即可求得点P的坐标。
②用待定系数法求出直线AC的解析式,由点Q在线段AC上,可设点Q的坐标为![]() ,从而由QD⊥x轴交抛物线于点D,得点D的坐标为
,从而由QD⊥x轴交抛物线于点D,得点D的坐标为![]() ,从而线段QD等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解。
,从而线段QD等于两点纵坐标之差,列出函数关系式应用二次函数最值原理求解。


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA全等,则AP= ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
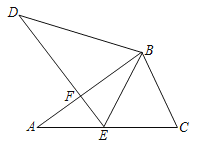
【题目】如图,已知∠A=∠D,AB=DB,点E在AC边上,∠AED=∠CBE,AB和DE相交于点F.
(1)求证:△ABC≌△DBE.
(2)若∠CBE=50°,求∠BED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
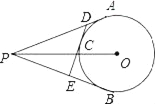
【题目】如图,PA、PB切⊙O于A、B,点C在弧AB上,DE切⊙O于C,交PA、PB于D、E,已知PO=13cm,⊙O的半径为5cm,则△PDE的周长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
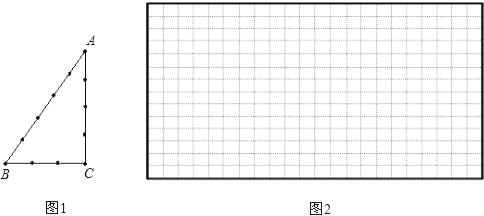
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)
A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方
B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形
(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数
(3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一个晾衣架放置在水平地面上,在其示意图中,支架OA、OB的长均为100cm,支架OA与水平晾衣架OC的夹角∠AOC为59°,则支架两个着地点之间的距离AB为_____cm.
(参考数据:sin59°≈0.86,cos59°≈0.52,tan59°≈1.66)

查看答案和解析>>
科目:初中数学 来源: 题型:
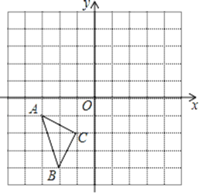
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
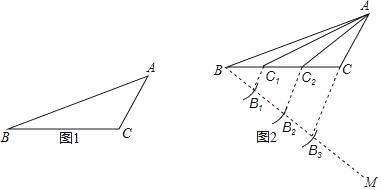
【题目】石景山区八角北路有一块三角形空地(如图1)准备绿化,拟从点A出发,将△ABC分成面积相等的三个三角形,栽种三种不同的花草.
下面是小美的设计(如图2).
作法:(1)作射线BM;
(2)在射线BM上顺次截取BB1=B1B2=B2B3;
(3)连接B3C,分别过B1、B2作B1C1∥B2C2∥B3C,交BC于点C1、C2;
(4)连接AC1、AC2.则![]() .
.
请回答,![]() 成立的理由是:
成立的理由是:
①_____;
②_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com