
����Ŀ��Ϊ����ʵ����������ƶ�����ߣ�A��B���Ǿ�����C��D�������ͷ�����֧��ũ����������֪A��B���ǹ��з���500�֣�����A�Ƿ��ϱ�B����100�֣���A����C��D�����˷��ϵķ��÷ֱ�Ϊ20Ԫ/�ֺ�25Ԫ/�֣���B����C��D�����˷��ϵķ��÷ֱ�Ϊ15Ԫ/�ֺ�24Ԫ/�֣���C����Ҫ����240�֣�D����Ҫ����260�֣�
��1��A�Ǻ�B�Ǹ��ж��ٶַ��ϣ�
��2�����A������C�����x�֣����˷�ΪyԪ������������˷ѣ�
��3�����ڸ������ͣ�ʹA������C����˷�ÿ�ּ���a��0��a��6��Ԫ����ʱ�������˲���ʹ���˷����٣�
���𰸡���1��A�Ǻ�B�Ƿֱ���200�ֺ�300�ַ��ϣ���2����A������D��200������B������C�����240�֣�����D��60��ʱ���˷����٣������˷���10040Ԫ����3����0��a<4ʱ�� A��200�ַ��϶�����D�磬B��240������C�磬60������D�磻��a=4ʱ����0��x��200��Χ�ڵ����ֵ��˷������ö�һ������4��a��6ʱ�� A��200�ַ��϶�����C�磬B��40������C�磬260������D��.
����������1������A��B���ǹ��з���500�֣�����A�Ƿ��ϱ�B����100�֣��з��̻���ô𰸣�
��2�����A������C�����x�֣��ú�x�Ĵ���ʽ�ֱ��ʾ����A��������D��ķ��϶�������B������C����϶���������B������D����϶��������ݣ��˷�=���������������ã���һ�κ�������ʽ������һ�κ��������ʵý��ۣ�
��3���г���A������C����˷�ÿ�ּ���a��0��a��6��Ԫʱ��һ�κ�������ʽ������һ�κ������������ۣ��ý��ۣ�
��1����A���л���a�֣�B���л���b����
�������⣬��![]() ��
��
���![]() ��
��
��A�Ǻ�B�Ƿֱ���200�ֺ�300�ַ��ϣ�
��2�����A������C�����x�֣�������D�磨200��x������
��B������C����ϣ�240��x���֣�������D�磨60+x������
�����˷�ΪyԪ���������⣬
��y=20x+25��200��x��+15��240��x��+24��60+x��=4x+10040��
�� ����0��x��200��
����0��x��200��
���ں�����һ�κ�����k=4��0��
���Ե�x=0ʱ���˷����٣������˷���10040Ԫ��
��3����A������C�����x�֣�����A������C����˷�ÿ�ּ���a��0��a��6��Ԫ��
����y=��20��a��x+25��200��x��+15��240��x��+24��60+x��=��4��a��x+10040��
��4��a>0ʱ����0��a<4ʱ��y����x����������൱x=0ʱ���˷�������A��200�ַ��϶�����D�磬B��240������C�磬60������D�磻
��4-a=0ʱ����a=4ʱ��y=10040����0��x��200��Χ�ڵ����ֵ��˷������ö�һ����
��4��a��0ʱ����4��a��6ʱ��y����x���������С���൱x=240ʱ���˷����٣���ʱA��200�ַ��϶�����C�磬B��40������C�磬260������D��.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��AB��ֱ��CD�ཻ�ڵ�O��OEƽ��![]() .
.
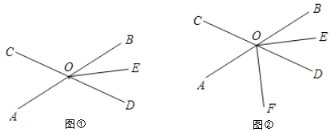
��1����ͼ�٣���![]() ����
����![]() �Ķ�����
�Ķ�����
��2����ͼ�ڣ�����OF��![]() �ڲ�.
�ڲ�.
����![]() ���ж�OF�Ƿ�Ϊ
���ж�OF�Ƿ�Ϊ![]() ��ƽ���ߣ���˵�����ɣ�
��ƽ���ߣ���˵�����ɣ�
����OFƽ��![]() ��
��![]() ����
����![]() �Ķ���.
�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�Ƕ��κ���y=ax2+bx+c��a��b��c�dz�����a��0��ͼ���һ���֣���x��Ľ���A�ڵ㣨2��0���ͣ�3��0��֮�䣬�Գ�����x=1����������˵������ab��0����2a+b=0����3a+c��0����a+b��m��am+b����mΪʵ������������1��x��3ʱ��y��0��������ȷ���ǣ�������

A. �٢ڢ� B. �٢ڢ� C. �ڢۢ� D. �ۢܢ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=120������һֱ�������ε�ֱ�ǣ���MON=90����������ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
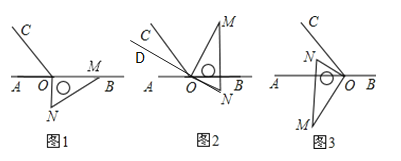
��1����ͼ1�У���NOC= ��
��2����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC���ʣ�NO���ӳ���OD�Ƿ�ƽ�֡�AOC����˵�����ɣ�
��3����ͼ1�е����ǰ��Ƶ�O��ÿ��6�����ٶ�����ʱ�뷽����תһ�ܣ�����ת�Ĺ����У���t��ʱ��ֱ��ONǡ��ƽ����ǡ�AOC����t��ֵΪ �룿��ֱ��д�������
��4����ͼ1�е����ǰ��Ƶ�O��ת��ͼ3��λ�ã�ʹON�ڡ�AOC���ڲ������AOM-��NOC= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
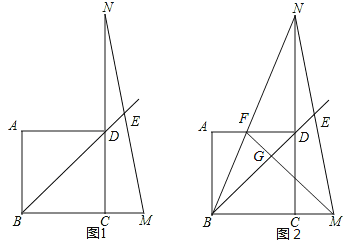
����Ŀ����ͼ1����������ABCD�У��ӳ�BC��M��ʹBM=DN������MN��BD�ӳ����ڵ�E��
��1����֤��BD+2DE=![]() BM��
BM��
��2����ͼ2������BN��AD�ڵ�F������MF��BD�ڵ�G����AF��FD=1��2����CM=2�����߶�DG= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���������Ƕ��κ���![]() ��a��0����ͼ�������н��ۣ���abc��0����b+2a=0������������x�����һ������Ϊ��4��0������a+c��b����3a+c��0��������ȷ�Ľ�����
��a��0����ͼ�������н��ۣ���abc��0����b+2a=0������������x�����һ������Ϊ��4��0������a+c��b����3a+c��0��������ȷ�Ľ�����
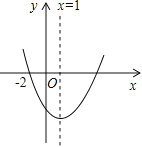
A. 5�� B. 4�� C. 3�� D. 2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ƽ�ٴ�ѧУ���̴���ӱ������Ϊ����Ůѧ������ס�ޣ����ÿ��ס4�ˣ���ô����30�������ţ����ÿ��ס8�ˣ���ô��һ�������Ҳ����������������ͳ���Ůѧ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
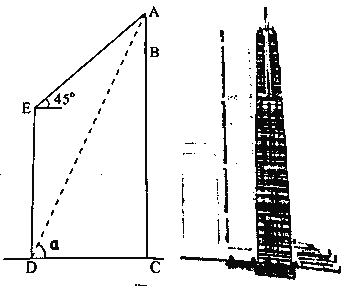
����Ŀ����ͼ����ɳ�����ֹ��ʽ���������¥![]() �ߴ�
�ߴ�![]() ����Ŀǰ����ʡ��һ��¥����������ͬһˮƽ���ϵĵڶ���¥
����Ŀǰ����ʡ��һ��¥����������ͬһˮƽ���ϵĵڶ���¥![]() ��
��![]() ��Ϊ�˲�����¥
��Ϊ�˲�����¥![]() �Ϸ�����
�Ϸ�����![]() �ĸ߶ȣ���¥
�ĸ߶ȣ���¥![]() ��
��![]() ����
����![]() ����������
������Ϊ����![]() ���ڶ���E���A������Ϊ
���ڶ���E���A������Ϊ![]() ��������
��������![]() �ĸ߶�.
�ĸ߶�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����ϣ����ݲ��ϻش�
����1��![]()
![]()
![]()
![]()
![]() .
.
����2��
8![]() ��0.125
��0.125![]() ��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��8��8��8��8��8��8��0.125��0.125��0.125��0.125��0.125��0.125
��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)��(8��0.125)
��(8��0.125)6 ��1.
��1������������ϵļ��㷽�����㣺![]() ��
��
��2��������ļ�����ܽ��һ�����ɣ�(����ĸ��ʾ) ![]() ��
��
��3���ã�2���Ĺ��ɼ��㣺![]() .
.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com