
【题目】直线AB与直线CD相交于点O,OE平分![]() .
.
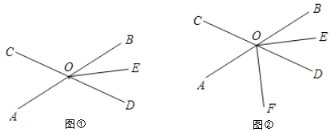
(1)如图①,若![]() ,求
,求![]() 的度数;
的度数;
(2)如图②,射线OF在![]() 内部.
内部.
①若![]() ,判断OF是否为
,判断OF是否为![]() 的平分线,并说明理由;
的平分线,并说明理由;
②若OF平分![]() ,
,![]() ,求
,求![]() 的度数.
的度数.
【答案】(1)∠AOE=155°;(2)①DF平分∠AOD,证明见解析;②∠BOD=60°
【解析】
(1)由∠BOC=130°可得∠BOD=50°根据OE平分∠BOD得![]() ,根据对顶角相等可得∠AOD=∠BOC=130°即可求出∠AOE的度数;
,根据对顶角相等可得∠AOD=∠BOC=130°即可求出∠AOE的度数;
(2)①由OE平分∠BOD可得∠BOE=∠DOE由OF⊥OE可得∠EOF=90°,故∠DOF=90°-∠DOE由图形可计算出:∠AOF=90°-∠BOE,故∠AOF=∠DOF可证DF平分∠AOD
②依题意设∠DOF=3x,则∠AOF=5x由OF平分∠AOE,可得∠EOF=∠AOF=5x,∠AOE=10x,可得:∠DOE=∠EOF-∠DOF=5x-3x=2x由OE平分∠BOD可得∠BOE=∠DOE=2x,∠BOD=4x由图形可知∠BOE+∠AOE=180°,列出方程求出x即可
(1) ∵∠BOC=130°
∴∠BOD=180°-∠BOC=180°-130°=50°
∵OE平分∠BOD
∴![]()
∴∠AOD=∠BOC=130°
∴∠AOE=∠AOD+∠DOE=130°+25°=155°
(2) ①∵OE平分∠BOD
∴∠BOE=∠DOE
∵OF⊥OE
∴∠EOF=90°
∴∠DOF=90°-∠DOE
∵∠AOF=180°-∠EOF-∠BOE
=180°-90°-∠BOE
=90°-∠BOE
∴∠AOF=∠DOF
∴DF平分∠AOD
②∵![]()
∴设∠DOF=3x,则∠AOF=5x
∵OF平分∠AOE
∴∠EOF=∠AOF=5x,∠AOE=10x
∴∠DOE=∠EOF-∠DOF=5x-3x=2x
∵OE平分∠BOD
∴∠BOE=∠DOE=2x,∠BOD=4x
∵∠BOE+∠AOE=180°
∴2x+10x=180°
∴x=15°
∴∠BOD=4×15°=60°


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是高,BE平分∠ABC.
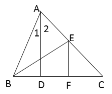
(1)若∠EBC=32°,∠1∶∠2=1∶2,EF∥AD,求∠FEC的度数.
(2)若∠2=50°,点F为射线CB上的一个动点,当△EFC为钝角三角形时,直接写出∠FEC的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干人乘坐若干辆汽车,如果每辆汽车坐22人,有1人不能上车;如果有一辆车不坐人,那么所有旅客正好能平分乘到其他各车上,则旅客共________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.附图(①)为一张三角形ABC纸片,P点在BC上.今将A折至P时,出现折线BD,其中D点在AC上,如图(②)所示.若△ABC的面积为80,△DBC的面积为50,则BP与PC的长度比为何?( )
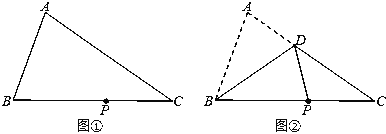
A.3:2 B.5:3 C.8:5 D.13:8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P是矩形ABCD的边AD上一个动点,矩形的两条边AB、BC的长分别为3和4,那么点P到矩形的两条对角线AC和BD的距离之和是( )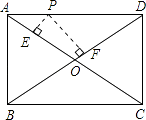
A.![]()
B.![]()
C.![]()
D.不确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,以△ABC的边AB、AC向外作正方形ABDE和正方形ACFG,试判断△ABC与△AEG面积之间的关系,并说明理由。

(2)园林小路,曲径通幽,如图2所示,小路由白色的正方形理石和黑色的三角形理石铺成.已知中间的所有正方形的面积之和是a平方米,内圈的所有三角形的面积之和是b平方米,这条小路一共占地多少平方米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
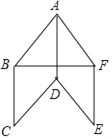
【题目】如图所示,已知四边形ABCD,ADEF都是菱形,∠BAD=∠FAD,∠BAD为锐角.
(1)求证:AD⊥BF;
(2)若BF=BC,求∠ADC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷![]() 份:
份:
(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含![]() 的代数式表示);
的代数式表示);
(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com