
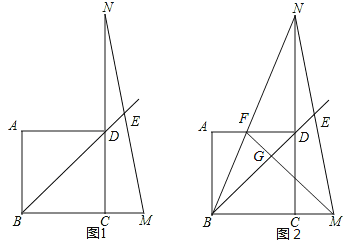
【题目】如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE=![]() BM.
BM.
(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG= .
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)根据结论可以猜想:要想解决问题需要把BD+2DE和BM转化到等腰直角三角形中去,因此想到过点M作BM的垂线与BD 的延长线交于点P,然后利用全等三角形的性质证明DE=PE即可证出结论;(2)由AB//CN可得:![]() ,所以DN=BM=2AB=2BC,又CM=2,所以BC=AD=CM=2,所以BD=
,所以DN=BM=2AB=2BC,又CM=2,所以BC=AD=CM=2,所以BD=![]() ,FD=
,FD=![]() ,由AD//BM可得:
,由AD//BM可得:![]() ,所以
,所以![]() ,因为BD=
,因为BD=![]() ,所以DG=
,所以DG=![]() .
.
试题解析:(1)证明:过点M作NP![]() BM,交BD 的延长线交于点P,
BM,交BD 的延长线交于点P,
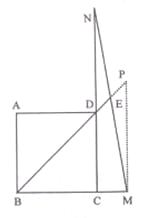
因为四边形ABCD是正方形,所以∠BCD =90°,∠DBC=∠BDC=45°,
所以PM∥CN,所以∠N=∠EMP,∠BDC=∠MPB=45°,
所以∠DBC=∠MPB,所以BM=MP,又因为BM=DN,所以DN=MP,
又因为∠N=∠EMP,∠NED=∠MEP,所以△NDE≌△MPE,所以DE=EP
由勾股定理可得:BP=![]() BM,即BD+2DE=
BM,即BD+2DE=![]() BM
BM
(2)DG=![]()


科目:初中数学 来源: 题型:
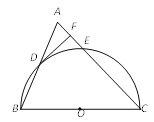
【题目】(9分)如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知第一象限内的点A在反比例函数y=![]() 的图象上,第二象限内的点B在反比例函数y=
的图象上,第二象限内的点B在反比例函数y=![]() 的图象上,且OA⊥OB,cosA=
的图象上,且OA⊥OB,cosA=![]() ,则k的值为( )
,则k的值为( )

A. -3 B. -6 C. -4 D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一个长方形休闲广场的四角都设计一块半径相同的四分之一圆形的花坛,若圆形的半径为![]() 米,广场的长为
米,广场的长为![]() 米,宽为
米,宽为![]() 米.
米.
(1)请列式表示花坛的面积和广场空地的面积;
(2)若休闲广场的长为500米,宽为200米,圆形花坛的半径为20米,求广场空地的面积;(计算结果保留![]() ;
;
(3)在(2)的情况下,若![]() 取3.14,求休闲广场的绿化率是多少?
取3.14,求休闲广场的绿化率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实党的“精准扶贫”政策,A、B两城决定向C、D两乡运送肥料以支持农村生产,已知A、B两城共有肥料500吨,其中A城肥料比B城少100吨,从A城往C、D两乡运肥料的费用分别为20元/吨和25元/吨;从B城往C、D两乡运肥料的费用分别为15元/吨和24元/吨.现C乡需要肥料240吨,D乡需要肥料260吨.
(1)A城和B城各有多少吨肥料?
(2)设从A城运往C乡肥料x吨,总运费为y元,求出最少总运费.
(3)由于更换车型,使A城运往C乡的运费每吨减少a(0<a<6)元,这时怎样调运才能使总运费最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知含字母a,b的代数式是:3[a2+2(b2+ab﹣2)]﹣3(a2+2b2)﹣4(ab﹣a﹣1)
(1)化简代数式;
(2)小红取a,b互为倒数的一对数值代入化简的代数式中,恰好计算得代数式的值等于0,那么小红所取的字母b的值等于多少?
(3)聪明的小刚从化简的代数式中发现,只要字母b取一个固定的数,无论字母a取何数,代数式的值恒为一个不变的数,那么小刚所取的字母b的值是多少呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B分别为数轴上的两点,A点对应的数为﹣20,B点对应的数为100.
![]()
(1)请写出与A,B两点距离相等的点M所对应的数 .
(2)现有一只电子蚂蚁P从B点出发,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度向右运动,x秒后两只电子蚂蚁在数轴上的C点相遇,请列方程求出x,并指出点C表示的数.
(3)若当电子蚂蚁P从B点出发时,以6单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以4单位/秒的速度也向左运动,y秒后两只电子蚂蚁在数轴上的D点相遇,请列方程求出y并指出点D表示的数.
查看答案和解析>>
科目:初中数学 来源: 题型:
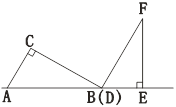
【题目】两个三角板ABC,DEF按如图所示的位置摆放,点B与点D重合,边AB与边DE在同一条直线上(假设图形中所有的点、线都在同一平面内),其中,∠C=∠DEF=90°,∠ABC=∠F=30°,AC=DE=4 cm.现固定三角板DEF,将三角板ABC沿射线DE方向平移,当点C落在边EF上时停止运动.设三角板平移的距离为![]() (cm),两个三角板重叠部分的面积为
(cm),两个三角板重叠部分的面积为![]() (cm2).
(cm2).
(1)当点C落在边EF上时,![]() =________cm;
=________cm;
(2)求![]() 关于
关于![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(3)设边BC的中点为点M,边DF的中点为点N,直接写出在三角板平移过程中,点M与点N之间距离的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com