
【题目】古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
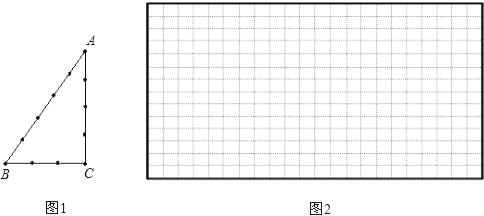
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)
A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方
B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形
(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数
(3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.)
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
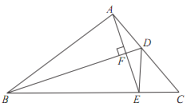
A.35°B.40°C.45°D.50°
查看答案和解析>>
科目:初中数学 来源: 题型:
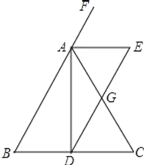
【题目】如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,ED∥AB交AC于点G,下列结论:①BD=DC;②AE∥BC;③AE=AG;④AG=![]() DE.正确的是_____(填写序号)
DE.正确的是_____(填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△BAD是由△BEC在平面内绕点B旋转60°而得,且AB⊥BC,BE=CE,连接DE.
(1)求证:△BDE≌△BCE;
(2)试判断四边形ABED的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与x轴相交于A、B两点,其中A点的坐标为(-3,0)。
与x轴相交于A、B两点,其中A点的坐标为(-3,0)。

(1)求点B的坐标;
(2)已知![]() ,C为抛物线与y轴的交点。
,C为抛物线与y轴的交点。
①若点P在抛物线上,且![]() ,求点P的坐标;
,求点P的坐标;
②设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值。
查看答案和解析>>
科目:初中数学 来源: 题型:
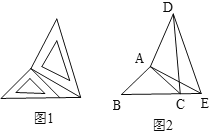
【题目】两个大小不同的等腰直角三角尺如图1所示放置,图2是由它抽象出的几何图形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() .
.
(1)请找出图2中与![]() 全等的三角形,并说明理由(说明:结论中不得含有未标识的字母);
全等的三角形,并说明理由(说明:结论中不得含有未标识的字母);
(2)判断线段![]() 与
与![]() 是否垂直,并说明理由.
是否垂直,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
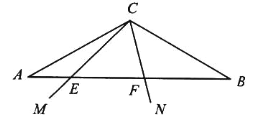
【题目】如图,在△ABC 中,∠A=∠B=30°,E,F 在 AB 上,∠ECF=60°.
(1)画出△BCF 绕点 C 顺时针旋转 120°后的△ACK;
(2)在(1)中,若 AE2+ EF2= BF2,求证 BF=![]() CF.
CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
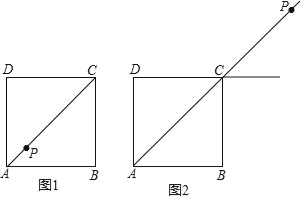
【题目】在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP.
(1)当点P在线段AC上时,如图1.
①依题意补全图1;
②若EQ=BP,则∠PBE的度数为 ,并证明;
(2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1,请写出求BE长的思路.(可以不写出计算结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com