
【题目】如图,在△ABC 中,∠A=∠B=30°,E,F 在 AB 上,∠ECF=60°.
(1)画出△BCF 绕点 C 顺时针旋转 120°后的△ACK;
(2)在(1)中,若 AE2+ EF2= BF2,求证 BF=![]() CF.
CF.
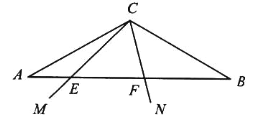
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)旋转后CB与CA重合,作∠KCA=∠FCB,截取KC=FC即可;(2)连结KE,作KH⊥AC于H,先得到∠ACE+∠BCF=60°,再根据旋转的性质得BF=AK,∠KCA=∠FCB,CK=CF,∠KAC=∠B=30°,则∠KCE=∠FCE,可根据“SAS”判断△CKE≌△CFE,所以KE=EF,由于AE2+EF2=BF2,则AE2+KE2=AK2,根据勾股定理的逆定理得∠AEK=90°,且∠KEC=∠FEC=45°,可计算∠BCF=45°,设KH=a,在Rt△KHC中可得KC=![]() a;在Rt△KHA中得AK=2a,所以AK:KC=2a:
a;在Rt△KHA中得AK=2a,所以AK:KC=2a:![]() a=
a=![]() ,则BF:CF=
,则BF:CF=![]() ,由此即可得结论.
,由此即可得结论.
(1)如图,
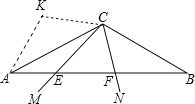
(2)证明:连结KE,作KH⊥AC于H,如图,
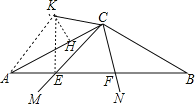
∵∠A=∠B=30°,∠MCN=60°,
∴∠ACB=120°,
∴∠ACE+∠BCF=60°,
∵△BCF绕点C顺时针旋转120゜后的△ACK,
∴BF=AK,∠KCA=∠FCB,CK=CF,∠KAC=∠B=30°,
∴∠KCE=∠KCA+∠ACE=∠FCB+∠ACE=60°,
∴∠KCE=∠FCE,
在△CKE和△CFE中,
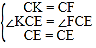 ,
,
∴△CKE≌△CFE,
∴KE=EF,∠KEC=∠FEC,
∵AE2+EF2=BF2,
∴AE2+KE2=AK2,
∴△AEK为直角三角形,
∴∠AEK=90°,
∴∠KEC=∠FEC=45°,
∴∠BCF=180°-45°-60°-30°=45°,
∴∠KCA=45°,
设KH=a,在Rt△KHC中,KC=![]() a;
a;
在Rt△KHA中,∠KAC =30°,
∴AK=2a,
∴AK:KC=2a:![]() a=
a=![]() ,
,
∴BF:CF=![]() ,
,
即BF=![]() CF.
CF.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
【题目】如图,是学习分式方程应用时,老师板书的问题和两名同学对该题的解答.(老师找聪聪和明明分别用不同的方法解答此题)

(1)聪聪同学所列方程中的![]() 表示_______________________________________.
表示_______________________________________.
(2)明明一时紧张没能做出来,请你帮明明完整的解答出来.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】古埃及人用下面的方法得到直角三角形,把一根长绳打上等距离的13个结(12段),然后用桩钉钉成一个三角形,如图1,其中∠C便是直角.
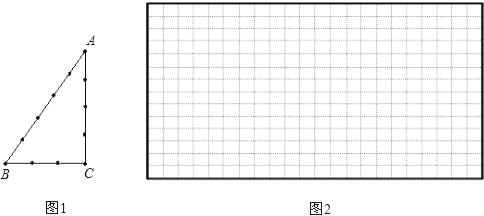
(1)请你选择古埃及人得到直角三角形这种方法的理由 (填A或B)
A.勾股定理:在直角三角形边的两直角边的平方和等于斜边的平方
B.勾股定理逆定理:如果三角形的三边长a、b、c有关系:a2+b2=c2,那么这个三角形是直角三角形
(2)如果三个正整数a、b、c满足a2+b2=c2,那么我们就称 a、b、c是一组勾股数,请你写出一组勾股数
(3)仿照上面的方法,再结合上面你写出的勾股数,你能否只用绳子,设计一种不同于上面的方法得到一个直角三角形(在图2中,只需画出示意图.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
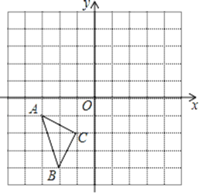
【题目】在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(﹣3,﹣1).
(1)将△ABC沿y轴正方向平移3个单位得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
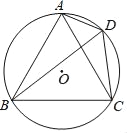
【题目】如图,四边形ABCD内接于⊙O,∠ABC=60°,BD平分∠ADC.
(1)试说明△ABC是等边三角形;
(2)若AD=2,DC=4,求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
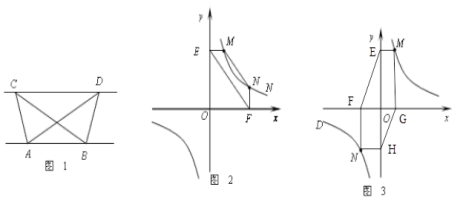
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由.
(2)结论应用:如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(3)变式探究:如图3,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
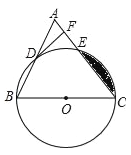
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D、E,DF⊥AC于点F.
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的半径为10,sinB=![]() ,求阴影部分面积.
,求阴影部分面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com