
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

【答案】(1)36,72;(2)①证明见解析;②CD=AN+CE,证明见解析.
【解析】
(1)根据题意可得△ABC,△BCD,△ABD都是等腰三角形,根据等腰三角形的性质可得∠A=∠DBA=∠DBC=![]() ∠ABC=
∠ABC=![]() ∠C,然后利用三角形的内角和即可得解;
∠C,然后利用三角形的内角和即可得解;
(2)①通过“角边角”证明△BNH≌△BEH,可得BN=BE,即可得证;
②根据题意可得AN=AB﹣BN=AC﹣BE,CE=BE﹣BC,CD=AC﹣AD=AC﹣BD=AC﹣BC,则可得CD=AN+CE.
解:(1)∵BD=BC,
∴∠BDC=∠C,
∵AB=AC,
∴∠ABC=∠C,
∴∠A=∠DBC,
∵AD=BD,
∴∠A=∠DBA,
∴∠A=∠DBA=∠DBC=![]() ∠ABC=
∠ABC=![]() ∠C,
∠C,
∵∠A+∠ABC+∠C=5∠A=180°,
∴∠A=36°,∠C=72°;
故答案为:36,72;
(2)①∵∠A=∠ABD=36°,∠B=∠C=72°,
∴∠ABD=∠CBD=36°,
∵BH⊥EN,
∴∠BHN=∠EHB=90°,
在△BNH与△BEH中,
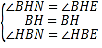 ,
,
∴△BNH≌△BEH(ASA),
∴BN=BE,
∴△BNE是等腰三角形;
②CD=AN+CE,理由:由①知,BN=BE,
∵AB=AC,
∴AN=AB﹣BN=AC﹣BE,
∵CE=BE﹣BC,
∴AN+BE=AC﹣BC,
∵CD=AC﹣AD=AC﹣BD=AC﹣BC,
∴CD=AN+CE.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:初中数学 来源: 题型:
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘(每个转盘分别被四等分和三等分),由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.
小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)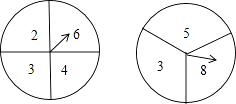
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数 ![]() 的图象如图所示,有下列5个结论:①
的图象如图所示,有下列5个结论:① ![]() ;②
;② ![]() ;③
;③ ![]() ;④
;④ ![]() ; ⑤
; ⑤ ![]() ,(
,( ![]() 的实数)其中正确的结论有( )
的实数)其中正确的结论有( )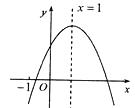
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
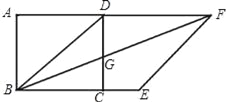
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC的底边BC长为4,面积是16,腰AC的垂直平分线EF分别交AC,AB边于E,F点,若点D为BC边的中点,点M为线段EF上一动点,则![]() 周长的最小值为______.
周长的最小值为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
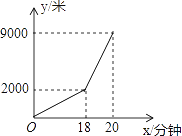
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,已知点![]() ,C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转
,C为y轴正半轴上一点,连接PC,线段PC绕点P顺时针旋转![]() 至线段PD,过点D作直线
至线段PD,过点D作直线![]() 轴,垂足为B,直线AB与直线OP交于点A,且
轴,垂足为B,直线AB与直线OP交于点A,且![]() ,直线CD与直线OP交于点Q,则点Q的坐标为______.
,直线CD与直线OP交于点Q,则点Q的坐标为______.
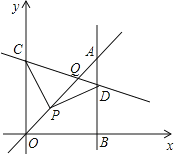
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.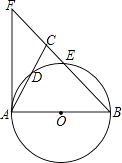
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com