
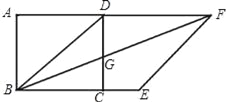
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
科目:初中数学 来源: 题型:
【题目】英国曼彻斯特大学的两位科学家因为成功地从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯目前是世上最薄却也是最坚硬的纳米材料,同时还是导电性最好的材料,其理论厚度仅0.000 000 000 34米,将这个数用科学记数法表示为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△ECD都是等腰直角三角形,CA=CB,CE=CD,△ABC的顶点A在△ECD的斜边DE上.
(1)求证AE2+AD2=2AC2 ;
(2)如图2,过点C作CO垂直AB于0点并延长交DE于点F,请确定线段AE、AF、DF间的数量关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )
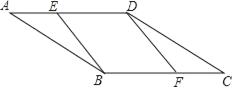
A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从﹣3,﹣2,﹣1,0,1,2,3这七个数中随机抽取一个数记为a,则a的值是不等式组 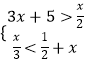 的解,但不是方程x2﹣3x+2=0的实数解的概率为 .
的解,但不是方程x2﹣3x+2=0的实数解的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长L与边长a的关系
C.长方形的长为a,宽为20,其面积S与a的关系
D.长方形的面积为40,长为a,宽为b,a与b的关系
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com