练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

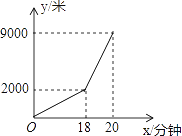
    【题目】小亮早晨从家骑车到学校，先上坡后下坡，所行路程y（米）与时间x（分钟）的关系如图所示，若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同，则小明从学校骑车回家用的时间是________分钟．

    【答案】63

    【解析】

    根据图表可计算出上坡的速度以及下坡的速度，又已知返回途中的上下坡的路程正好相反，故可计算出共用的时间．

    由图可得，去校时，上坡路的距离为2000米，所用时间为18分，

    ∴上坡速度=2000÷18=米/分，

    下坡路的距离是9000-2000=7000米，所用时间为20-18=2分，

    ∴下坡速度=7000÷2=3500米/分；

    ∵去学校时的上坡回家时变为下坡、去学校时的下坡回家时变为上坡，

    ∴小明从学校骑车回家用的时间是：7000÷+2000÷3500=63+=63分钟．

    故答案为：63．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，在Rt△OAB中，∠OAB=90°，∠BOA=30°，AB=2．若以O为坐标原点，OA所在直线为x轴，建立如图所示的平面直角坐标系，点B在第一象限内．将Rt△OAB沿OB折叠后，点A落在第一象限内的点C处．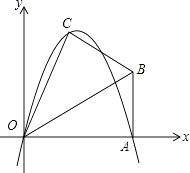

    （1）求点C的坐标；
    （2）若抛物线y=ax2+bx（a≠0）经过C、A两点，求此抛物线的解析式；
    （3）若上述抛物线的对称轴与OB交于点D，点P为线段DB上一动点，过P作y轴的平行线，交抛物线于点M，问：是否存在这样的点P，使得四边形CDPM为等腰梯形？若存在，请求出此时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平行四边形ABCD中，E，F分别为AD，BC边上的一点，增加下列条件，不能得出BE∥DF的是（　　）

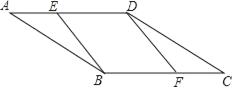
    A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了创建全国卫生城市，某社区要清理一个卫生死角内的垃圾，租用甲、乙两车运送，两车各运12趟可完成，需支付运费4800元．已知甲、乙两车单独运完此堆垃圾，乙车所运趟数是甲车的2倍，且乙车每趟运费比甲车少200元．

    （1）求甲、乙两车单独运完此堆垃圾各需运多少趟？

    （2）若单独租用一台车，租用哪台车合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，D在边AC上，且．

    如图1，填空______，______

    如图2，若M为线段AC上的点，过M作直线于H，分别交直线AB、BC与点N、E．

    求证：是等腰三角形；

    试写出线段AN、CE、CD之间的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

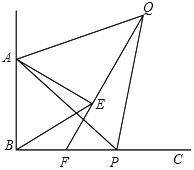
    【题目】如图，，P为射线BC上任意一点点P和点B不重合，分别以AB，AP为边在内部作等边和等边，连结QE并延长交BP于点F，连接EP，若，，则______．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】从﹣3，﹣2，﹣1，0，1，2，3这七个数中随机抽取一个数记为a，则a的值是不等式组 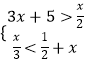的解，但不是方程x2﹣3x+2=0的实数解的概率为 ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在矩形ABCD中，AB=3，BC=2，点F是BC的中点，点E是边AB上一点，且BE=2，连结DE，EF，并以DE，EF为边作EFGD，连结BG，分别交EF和DC于点M，N，则 = ．

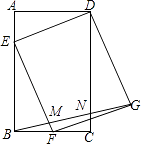
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：△ABC是等腰直角三角形，动点P在斜边AB所在的直线上，以PC为直角边作等腰直角三角形PCQ，其中∠PCQ=90°，探究并解决下列问题：
    （1）如图①，若点P在线段AB上，且AC=1+ ，PA= ，则：

    ① 线段PB= ， PC= ；
    ② 猜想：PA2 ， PB2 ， PQ2三者之间的数量关系为；
    （2）如图②，若点P在AB的延长线上，在（1）中所猜想的结论仍然成立，请你利用图②给出证明过程；

    （3）若动点P满足 = ，求 的值．（提示：请利用备用图进行探求）

    查看答案和解析>>

    同步练习册答案