
【题目】已知,在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2.若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内.将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.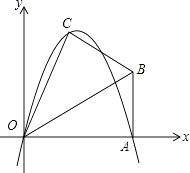
(1)求点C的坐标;
(2)若抛物线y=ax2+bx(a≠0)经过C、A两点,求此抛物线的解析式;
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作y轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
【答案】
(1)解:过点C作CH⊥x轴,垂足为H;
∵在Rt△OAB中,∠OAB=90°,∠BOA=30°,AB=2,
∴OB=4,OA=2 ![]() ;
;
由折叠的性质知:∠COB=30°,OC=AO=2 ![]() ,
,
∴∠COH=60°,OH= ![]() ,CH=3;
,CH=3;
∴C点坐标为( ![]() ,3)
,3)
(2)解:∵抛物线y=ax2+bx(a≠0)经过C( ![]() ,3)、A(2
,3)、A(2 ![]() ,0)两点,
,0)两点,
∴ ![]() ,
,
解得 ![]() ;
;
∴此抛物线的函数关系式为:y=﹣x2+2 ![]() x
x
(3)解:存在.
∵y=﹣x2+2 ![]() x的顶点坐标为(
x的顶点坐标为( ![]() ,3),
,3),
即为点C,MP⊥x轴,垂足为N,设PN=t;
∵∠BOA=30°,
∴ON= ![]() t,
t,
∴P( ![]() t,t);
t,t);
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E;
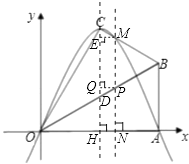
把x= ![]() t代入y=﹣x2+2
t代入y=﹣x2+2 ![]() x,
x,
得y=﹣3t2+6t,
∴M( ![]() t,﹣3t2+6t),E(
t,﹣3t2+6t),E( ![]() ,﹣3t2+6t),
,﹣3t2+6t),
同理:Q( ![]() ,t),D(
,t),D( ![]() ,1);
,1);
要使四边形CDPM为等腰梯形,只需CE=QD,
即3﹣(﹣3t2+6t)=t﹣1,
解得t= ![]() ,t=1(舍去),
,t=1(舍去),
∴P点坐标为( ![]() ,
, ![]() ),
),
∴存在满足条件的P点,使得四边形CDPM为等腰梯形,此时P点坐标为( ![]() ,
, ![]() )
)
【解析】(1)根据直角三角形的性质,求出OA、OB的值,由折叠的性质,得到C点坐标;(2)由抛物线经过C、A两点,由待定系数法求出抛物线的函数关系式;(3)根据抛物线的解析式,求出抛物线的顶点坐标,由∠BOA=30°,得到P点的坐标,求出M、E、Q、D的坐标,根据要使四边形CDPM为等腰梯形,只需CE=QD,求出P点坐标;此题是综合题,难度较大,计算和解方程时需认真仔细.


科目:初中数学 来源: 题型:
【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:
作物种类 | 每公顷所需人数/人 | 每公顷投入资金/万元 |
蔬菜 | 4 | 2 |
水果 | 5 | 3 |
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
查看答案和解析>>
科目:初中数学 来源: 题型:
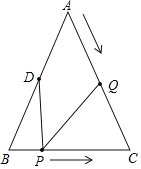
【题目】如图,已知![]() 中,
中,![]() ,
,![]() ,点D为AB的中点,如果点P在线段BC上以
,点D为AB的中点,如果点P在线段BC上以![]() 的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C以
的速度由点B向点C运动,同时,点Q在线段AC上由点A向点C以![]() 的速度运动
的速度运动![]() 若点P、Q两点分别从点B、A同时出发.
若点P、Q两点分别从点B、A同时出发.
![]() 经过2秒后,求证:
经过2秒后,求证:![]() ≌
≌![]()
![]() 若
若![]() 的周长为18cm,问经过几秒钟后,
的周长为18cm,问经过几秒钟后,![]() 为等腰三角形?
为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年(4)班要举行一场毕业联欢会,主持人同时转动下图中的两个转盘(每个转盘分别被四等分和三等分),由一名同学在转动前来判断两个转盘上指针所指的两个数字之和是奇数还是偶数,如果判断错误,他就要为大家表演一个节目;如果判断正确,他可以指派别人替自己表演节目.现在轮到小明来选择,小明不想自己表演,于是他选择了偶数.
小明的选择合理吗?从概率的角度进行分析(要求用树状图或列表方法求解)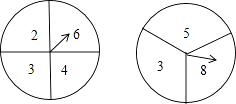
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数y= ![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k=( )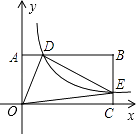
A.![]()
B.![]()
C.![]()
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.
(1)如图1,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;
(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由;
(3)如图3,当点D在边BC的反向延长线上且其他条件不变时,补全图形,并直接写出AC、CE、CD之间存在的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
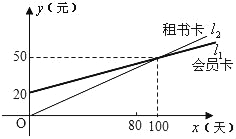
【题目】某图书馆开展两种方式的租书业务:一种是使用会员卡,另一种是使用租书卡,使用这两种卡租一本书,租书金额y(元)与租书时间x(天)之间的关系如图所示:
(1)用租书卡每天租书的收费为 元,用会员卡每天租书的收费是 元;
(2)分别写出用租书卡和会员卡租书的金额y1、y2与租书时间x之间的函数关系式;
(3)如果租书50天,选择哪种租书方式比较划算?如果花费80元租书,选择哪种租书方式比较划算?
查看答案和解析>>
科目:初中数学 来源: 题型:
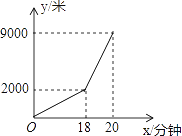
【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com