
����Ŀ����֪��ABCΪ�ȱ������Σ���DΪֱ��BC�ϵ�һ����(��D����B��C�غ�)����ADΪ�����ȱߡ�ADE(����A��D��E����ʱ�뷽������)������CE��
(1)��ͼ1������D�ڱ�BC��ʱ����֤����BD��CE����AC��CE+CD��
(2)��ͼ2������D�ڱ�BC���ӳ�������������������ʱ������AC��CE+CD�Ƿ������������������д��AC��CE��CD֮����ڵ�������ϵ����˵�����ɣ�
(3)��ͼ3������D�ڱ�BC�ķ����ӳ�������������������ʱ����ȫͼ�Σ���ֱ��д��AC��CE��CD֮����ڵ�������ϵ��

���𰸡�(1)��֤������������֤����������(2)AC��CE+CD��������AC��CE��CD֮����ڵ�������ϵ�ǣ�AC��CE��CD�����ɼ�������(3)��ͼ��������AC��CD��CE��
��������
��1�����ݵȱ������ε����ʼ���ʽ������֤����ABD�ա�ACE���Ӷ��ó����ۣ�
��2�����ݵȱ������ε����ʼ���ʽ�����ʾͿ��Եó���ABD�ա�ACE���Ϳ��Եó�BD��CE���Ϳ��Եó�AC��CE��CD��
��3���ȸ�����������ͼ�Σ����ݵȱ������ε����ʼ���ʽ�����ʾͿ��Եó���ABD�ա�ACE���Ϳ��Եó�BD��CE���Ϳ��Եó�AC��CD��CE��
(1)�ߡ�ABC�͡�ADE���ǵȱ������Σ�
��AB��AC��BC��AD��AE����BAC����DAE��60�㣮
���BAC����CAD����DAE����CAD������BAD����CAE��
�ڡ�ABD�͡�ACE�У�
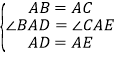 ��
��
���ABD�ա�ACE(SAS)��
��BD��CE��
��BC��BD+CD��AC��BC��
��AC��CE+CD��
(2)AC��CE+CD��������
AC��CE��CD֮����ڵ�������ϵ�ǣ�AC��CE��CD��
���ɣ��ߡ�ABC�͡�ADE���ǵȱ������Σ�
��AB��AC��BC��AD��AE����BAC����DAE��60�㣮
���BAC+��CAD����DAE+��CAD��
���BAD����CAE
�ڡ�ABD�͡�ACE�У�
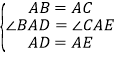
���ABD�ա�ACE(SAS)
��BD��CE
��CE��CD��BD��CD��BC��AC��
��AC��CE��CD��
(3)��ȫͼ��(��ͼ)
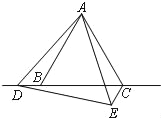
AC��CE��CD֮����ڵ�������ϵ�ǣ�AC��CD��CE��
���ɣ��ߡ�ABC�͡�ADE���ǵȱ������Σ�
��AB��AC��BC��AD��AE����BAC����DAE��60�㣮
���BAC����BAE����DAE����BAE��
���BAD����CAE
�ڡ�ABD�͡�ACE�У�
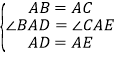
���ABD�ա�ACE(SAS)
��BD��CE��
��BC��CD��BD��
��BC��CD��CE��
��AC��CD��CE��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס���������ͬһƽֱ��·��![]() ��������ʻ(��;��ͣ��)��ǰ���յ�
��������ʻ(��;��ͣ��)��ǰ���յ�![]() �أ��ס�������֮��ľ���
�أ��ס�������֮��ľ���![]() (ǧ��)��׳���ʻ��ʱ��
(ǧ��)��׳���ʻ��ʱ��![]() (Сʱ)֮��ĺ�����ϵ��ͼ��ʾ������˵�����ټס����������210ǧ�ף��ڼ��ٶ�Ϊ60ǧ��/Сʱ�������ٶ�Ϊ120ǧ��/Сʱ�����ҳ�����ʻ
(Сʱ)֮��ĺ�����ϵ��ͼ��ʾ������˵�����ټס����������210ǧ�ף��ڼ��ٶ�Ϊ60ǧ��/Сʱ�������ٶ�Ϊ120ǧ��/Сʱ�����ҳ�����ʻ![]() Сʱ��������ȷ�ĸ���Ϊ( )
Сʱ��������ȷ�ĸ���Ϊ( )
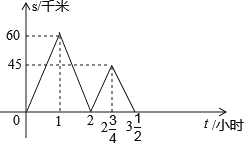
A. 1��B. 2��C. 3��D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ӣ������˹�ش�ѧ����λ��ѧ����Ϊ�ɹ��ش�ʯī�з����ʯīϩ���ٻ���ŵ��������ѧ����ʯīϩĿǰ�������ȴҲ�����Ӳ�����ײ��ϣ�ͬʱ���ǵ�������õIJ��ϣ������ۺ�Ƚ�0.000 000 000 34�ף���������ÿ�ѧ��������ʾΪ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��OAB�У���OAB=90�㣬��BOA=30�㣬AB=2������OΪ����ԭ�㣬OA����ֱ��Ϊx�ᣬ������ͼ��ʾ��ƽ��ֱ������ϵ����B�ڵ�һ�����ڣ���Rt��OAB��OB�۵���A���ڵ�һ�����ڵĵ�C����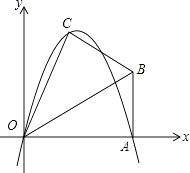
��1�����C�����ꣻ
��2����������y=ax2+bx��a��0������C��A���㣬��������ߵĽ���ʽ��
��3�������������ߵĶԳ�����OB���ڵ�D����PΪ�߶�DB��һ���㣬��P��y���ƽ���ߣ����������ڵ�M���ʣ��Ƿ���������ĵ�P��ʹ���ı���CDPMΪ�������Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʦ��������ҵ��������һ����ʽ�ļ����⣺![]() ���ס�����λͬѧ��ɵĹ��̷ֱ����£�
���ס�����λͬѧ��ɵĹ��̷ֱ����£�

��ʦ��������λͬѧ�Ľ���д���
(1)��ͬѧ�Ľ��ӵ��� ������ʼ���ִ������ԭ������ ����
��ͬѧ�Ľ��ӵ��� ������ʼ���ִ������ԭ������ ����
(2)������д����ɴ������ȷ�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ����֯���꼶400��ѧ���μ�����Ӫ����֪��3��С�ͳ���1����ͳ�ÿ�ο�����ѧ��105�ˣ���1��С�ͳ���2����ͳ�ÿ�ο�����ѧ��110��
��1��ÿ��С�ͳ���ÿ����ͳ�������������ѧ����
��2����ѧУ�ƻ�����С�ͳ�a������ͳ�b����һ�����꣬��ǡ��ÿ������������
�����![]() ��
��![]() ����Ĺ�ϵʽ__________��
����Ĺ�ϵʽ__________��
����С�ͳ�ÿ�����2000Ԫ����ͳ�ÿ�����3800Ԫ��������Ƴ���ʡǮ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����ABC����ECD���ǵ���ֱ�������Σ�CA=CB��CE=CD����ABC�Ķ���A����ECD��б��DE��.
(1)��֤AE2+AD2=2AC2 ��
(2)��ͼ2������C��CO��ֱAB��0�㲢�ӳ���DE�ڵ�F����ȷ���߶�AE��AF��DF���������ϵ����֤����Ľ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�E��F�ֱ�ΪAD��BC���ϵ�һ�㣬�����������������ܵó�BE��DF���ǣ�������
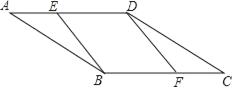
A. AE=CF B. BE=DF C. ��EBF=��FDE D. ��BED=��BFD
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ө�3����2����1��0��1��2��3���߸����������ȡһ������Ϊa����a��ֵ�Dz���ʽ�� 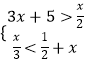 �Ľ⣬�����Ƿ���x2��3x+2=0��ʵ����ĸ���Ϊ ��
�Ľ⣬�����Ƿ���x2��3x+2=0��ʵ����ĸ���Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com