
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则:
,则:
① 线段PB= , PC= ;
② 猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
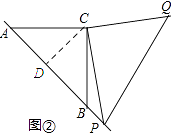
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
【答案】
(1)![]() ,2,AP2+BP2=PQ2
,2,AP2+BP2=PQ2
(2)解:如图②:过点C作CD⊥AB,垂足为D.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD+PD)2=(DC+PD)2=CD2+2DCPD+PD2,
PB2=(DP﹣BD)2=(PD﹣DC)2=DC2﹣2DCPD+PD2,
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2.
(3)解:如图③:过点C作CD⊥AB,垂足为D.

①当点P位于点P1处时.
∵ ![]() ,
,
∴ ![]() .
.
∴ ![]() .
.
在Rt△CP1D中,由勾股定理得: ![]() =
= ![]() =
= ![]() DC,
DC,
在Rt△ACD中,由勾股定理得:AC= ![]() =
= ![]() =
= ![]() DC,
DC,
∴ ![]() .
.
②当点P位于点P2处时.
∵ ![]() =
= ![]() ,
,
∴ ![]() .
.
在Rt△CP2D中,由勾股定理得: ![]() =
= ![]() =
= ![]() ,
,
在Rt△ACD中,由勾股定理得:AC= ![]() =
= ![]() =
= ![]() DC,
DC,
∴ ![]() .
.
综上所述, ![]() 的比值为
的比值为 ![]() 或
或 ![]() .
.
【解析】(1)如图①:

①∵△ABC是等腰直直角三角形,AC=1+ ![]()
∴AB= ![]() =
= ![]() =
= ![]() +
+ ![]() ,
,
∵PA= ![]() ,
,
∴PB= ![]() ,
,
∵△ABC和△PCQ均为等腰直角三角形,
∴AC=BC,PC=CQ,∠ACP=∠BCQ,
∴△APC≌△BQC.
∴BQ=AP= ![]() ,∠CBQ=∠A=45°.
,∠CBQ=∠A=45°.
∴△PBQ为直角三角形.
∴PQ= ![]() .
.
∴PC= ![]() PQ=2.
PQ=2.
所以答案是: ![]() ,2;
,2;
②如图1.
∵△ACB为等腰直角三角形,CD⊥AB,
∴CD=AD=DB.
∵AP2=(AD﹣PD)2=(DC﹣PD)2=DC2﹣2DCPD+PD2,PB2=(DB+PD)2=(DC+DP)2=CD2+2DCPD+PD2
∴AP2+BP2=2CD2+2PD2,
∵在Rt△PCD中,由勾股定理可知:PC2=DC2+PD2,
∴AP2+BP2=2PC2.
∵△CPQ为等腰直角三角形,
∴2PC2=PQ2.
∴AP2+BP2=PQ2


科目:初中数学 来源: 题型:
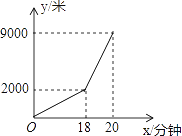
【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一元二次方程ax2+bx+c=0中,若a>0,b<0,c<0,则这个方程根的情况是( )
A.有两个正根
B.有两个负根
C.有一正根一负根且正根绝对值大
D.有一正根一负根且负根绝对值大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.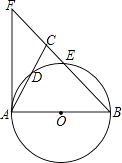
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(b2)3(b3)4÷(﹣b5)3
(2)(![]() )﹣1+(π﹣2018)0﹣(﹣1)2019
)﹣1+(π﹣2018)0﹣(﹣1)2019
(3)(3﹣x)(﹣x+3)﹣x(x+1)
(4)(2a+b﹣5)(2a﹣b﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A.3sin40°
B.3sin50°
C.3tan40°
D.3tan50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家距离学校8千米,今天早晨,小明骑车上学图中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系.请根据图象,解答下列问题:

(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明从早晨出发直到到达学校共用了多少分钟?
(3)小明修车前、后的行驶速度分别是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com