
【题目】已知△ABC中,BC=6,AB、AC的垂直平分线分别交边BC于点M、N,若MN=2,则△AMN的周长是_____.
【答案】6或10
【解析】
由直线PM为线段AB的垂直平分线,根据线段垂直平分线定理:线段垂直平分线上的点到线段两端点的距离相等可得AM=BM,同理可得AN=NC,然后表示出三角形AMN的三边之和,等量代换可得其周长等于BC的长,由BC的长即可得到三角形AMN的周长.
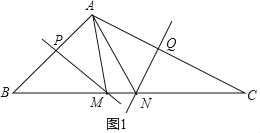
如图1,∵直线MP为线段AB的垂直平分线,
∴MA=MB,
又直线NQ为线段AC的垂直平分线,
∴NA=NC,
∴△AMN的周长l=AM+MN+AN=BM+MN+NC=BC,
又BC=6,
则△AMN的周长为6;
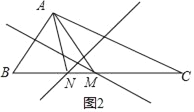
如图2,△AMN的周长l=AM+MN+AN=BM+MN+NC=BC+2MN,
又BC=6,
则△AMN的周长为10,
故答案为:6或10.


科目:初中数学 来源: 题型:
【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作EFGD,连结BG,分别交EF和DC于点M,N,则 ![]() = .
= . 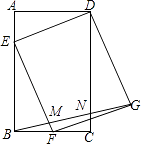
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 1 是一个长为 4a、宽为 b 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图 2).
(1)图 2 中的阴影部分的面积为 ;(用 a、b 的代数式表示)
(2)观察图 2 请你写出a b2 、a b2 、ab 之间的等量关系是 ;
(3)根据⑵中的结论,若 x y 5 , x y ![]() ,则 x y2 =_______.
,则 x y2 =_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长L与边长a的关系
C.长方形的长为a,宽为20,其面积S与a的关系
D.长方形的面积为40,长为a,宽为b,a与b的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一劳动节大酬宾!”,某商场设计的促销活动如下:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”、“10元”、“20元”和“50元”的字样.规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两小球所标金额的和返还相等价格的购物券,购物券可以在本商场消费.某顾客刚好消费300元.
(1)该顾客至多可得到元购物券;
(2)请你用画树状图或列表的方法,求出该顾客所获得购物券的金额不低于50元的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则:
,则:
① 线段PB= , PC= ;
② 猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
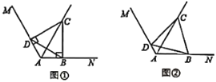
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com