
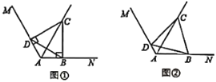
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
【答案】(1)∠CDB=60°.(2)见解析
【解析】
(1)利用四边形的内角和即可得出∠BCD的度数,再利用角平分线的性质定理即可得出CD=CB,△BCD是等边三角形,即可求解;
(2)先判断出∠CDE=∠ABC,进而得出△CDE≌△CBF(AAS),再根据分割面积法证明四边形ABCD的面积是定值即可.
(1)∵射线AC是∠MAN的角平分线,∠NAC=60°,
∴∠MAN=120°,
∵∠ABC=∠ADC=90°,
根据四边形的内角和得,∠BCD=360°(∠ABC+∠ADC+∠MAN)=60°,
∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,
∴CD=CB(角平分线的性质定理),
∴△BCD是等边三角形;
∴∠CDB=60°.
(2)如图②,同(1)得出,∠BCD=60°,
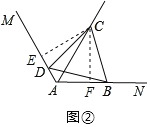
过点C作CE⊥AM于E,CF⊥AN于F,
∵AC是∠MAN的平分线,
∴CE=CF,
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,
在△CDE和△CFB中,
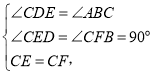
∴△CDE≌△CBF(AAS),
S四边形ABCD![]()
∴四边形ABCD的面积是个定值.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】计算题
(1)计算: ![]() (
( ![]() ﹣
﹣ ![]() )﹣
)﹣ ![]() ﹣|
﹣| ![]() ﹣3|
﹣3|
(2)计算:(﹣1)2014﹣ ![]() sin45°+(π﹣3.14)0
sin45°+(π﹣3.14)0
(3)解方程:2x2+x﹣6=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】清明节假期的某天,小强骑车从家出发前往革命烈士陵园扫墓,匀速行驶一段时间后,因车子出现问题,途中耽搁了一段时间,车子修好后,以更快的速度匀速前行,到达烈士陵园扫完墓后匀速骑车回家.其中![]() 表示小强从家出发后的时间,
表示小强从家出发后的时间,![]() 表示小强离家的距离,下面能反映变量
表示小强离家的距离,下面能反映变量![]() 与
与![]() 之间关系的大致图象是( )
之间关系的大致图象是( )
A.  B.
B. 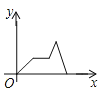
C.  D.
D. 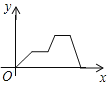
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明家距离学校8千米,今天早晨,小明骑车上学图中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系.请根据图象,解答下列问题:

(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明从早晨出发直到到达学校共用了多少分钟?
(3)小明修车前、后的行驶速度分别是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某中学准备在校园里利用围墙的一段,再砌三面墙,围成一个矩形花园ABCD(围墙MN最长可利用25m),现在已备足可以砌50m长的墙的材料,试设计一种砌法,使矩形花园的面积为300m2 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示.现将△ABC平移,使点A变换为点D,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并求△DEF的面积.
(2)若连接AD、CF,则这两条线段之间的关系是 ;
(3)请在AB上找一点P,使得线段CP平分△ABC的面积,在图上作出线段CP.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com