
【题目】已知非负数a、b、c满足![]() ,代数式3a+4b+5c的最大值是x,最小值是y,则x+y的值是___________.
,代数式3a+4b+5c的最大值是x,最小值是y,则x+y的值是___________.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=3,BC=2,点F是BC的中点,点E是边AB上一点,且BE=2,连结DE,EF,并以DE,EF为边作EFGD,连结BG,分别交EF和DC于点M,N,则 ![]() = .
= . 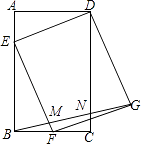
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则:
,则:
① 线段PB= , PC= ;
② 猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边BC=20,面积为120,点F在边BC上,且BF=3FC,EG是腰AC的垂直平分线,若点D在EG上运动,则△CDF周长的最小值为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:
(1)∠GAF等于多少度?为什么?
(2)EF与FG相等吗?为什么?
(3)△AEF与△AGF有何种位置关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )

A.nB.2n-1C.![]() D.3(n+1)
D.3(n+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
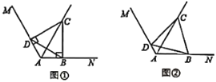
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是![]() 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下![]() 型与
型与![]() 型两种板材.如图所示,(单位:
型两种板材.如图所示,(单位:![]() )
)

(1)列出方程(组),求出图甲中![]() 与
与![]() 的值.
的值.
(2)在试生产阶段,若将![]() 张标准板材用裁法一裁剪,
张标准板材用裁法一裁剪,![]() 张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒![]() 个,横式无盖礼品盒的
个,横式无盖礼品盒的![]() 个,根据题意完成表格:
个,根据题意完成表格:
礼品盒板 材 | 竖式无盖(个) | 横式无盖(个) |
|
| |
A型(张) |
|
|
B型(张) |
|

③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个(在横线上直接写出答案,无需书写过程)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com