
【题目】如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:
(1)∠GAF等于多少度?为什么?
(2)EF与FG相等吗?为什么?
(3)△AEF与△AGF有何种位置关系?

【答案】解:(1)∠GAF=45°;(2)EF=FG;(3)△AEF与△AGF关于直线AF轴对称.
【解析】
(1)由旋转的性质可知△ADE≌△ABG,可知AE=AG,∠DAE=∠BAG,故∠GAF=∠GAB+∠BAF=∠DAE+∠BAF=∠BAD-∠EAF;
(2)由(1)可知∠EAF=∠GAF,且AE=AG,AF=AF,可证△AEF≌△AGF,从而得EF=FG;
(3)根据(2)可知△AEF≌△AGF.
解:(1)∠GAF=45°.
∵△ABG是将△ADE绕A点顺时针旋转90°得到的,
∴∠DAE=∠BAG,
∵∠EAF=45°,∠BAD=90°,
∴∠DAE+∠FAB=90°﹣45°=45°,
∴∠BAG+∠FAB=45°,即∠GAF=45°;
(2)EF=FG.
理由:∵△ABG是△ADE旋转90°得到的,
∴AE=AG,
∵∠EAF=45°,∠GAF=45°,
∴∠EAF=∠GAF,
在△AEF和△AGF中,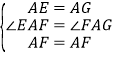 ,
,
∴△AEF≌△AGF,
∴EF=FG;
(3)△AEF与△AGF关于直线AF轴对称.
由△AEF≌△AGF易证.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BA=BC,以AB为直径的⊙O分别交AC,BC于点D,E,延长BC到点F,连接AF,使∠ABC=2∠CAF.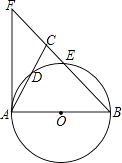
(1)求证:AF是⊙O的切线;
(2)若AC=4,CE:EB=1:3,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角三角形ABC中,已知∠C=90°,∠A=40°,BC=3,则AC=( )
A.3sin40°
B.3sin50°
C.3tan40°
D.3tan50°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的函数图象反映的过程是:李大爷每天早上都到公园锻炼,他从家去公园锻炼一会儿,又去了菜市场后马上回家,其中![]() 表示时间,
表示时间,![]() 表示李大爷离他家的距离。
表示李大爷离他家的距离。
(1)李大爷家到公园的距离是多少千米,他在公园银炼了多少小时;
(2)李大爷从菜市场回家的平均速度;
(3)李大爷从家到菜市场的平均速度。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分8分)
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(k-1)x2+2x-2=0有两个不相等的实数根,则k的取值范围是( )
A.k> ![]()
B.k≥ ![]()
C.k> ![]() 且k≠1
且k≠1
D.k≥ ![]() 且k≠1
且k≠1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com