
【题目】已知,AB//ED, BF平分∠ABC, DF平分∠EDC.
(1)若∠ABC =130°,∠EDC=110°,求∠C的度数和∠BFD的度数;
(2)请直接写出∠BFD与∠C的关系.

【答案】(1)![]()
![]()
![]()
![]()
【解析】
(1)过点C作CN//AB,过点F作FM//AB,根据平行线的性质得![]()
![]()
![]() 根据∠ABC =130°,∠EDC=110°,即可求出
根据∠ABC =130°,∠EDC=110°,即可求出
∠C的度数;根据角平分线的性质求出![]()
![]() 根据平行线的性质求出
根据平行线的性质求出![]()
![]() 即可求出∠BFD的度数;
即可求出∠BFD的度数;
(2)参照(1)的解题思路进行求解即可.
(1)如图,过点C作CN//AB,过点F作FM//AB.
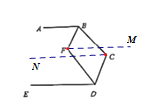
![]() CN//AB,
CN//AB,
![]()
![]()
![]() AB//ED
AB//ED
![]() CN//ED
CN//ED
![]()
![]()
∠ABC =130°,∠EDC=110°,
![]()
![]()
![]() BF平分∠ABC, DF平分∠EDC,
BF平分∠ABC, DF平分∠EDC,
![]()
![]()
![]() FM//AB.
FM//AB.
![]()
![]() AB//ED.
AB//ED.
![]() FM//ED
FM//ED
![]()
![]()
∠BCD的度数和∠BFD的度数均为![]() ;
;
(2)![]()
理由如下:
![]() CN//AB,
CN//AB,
![]()
![]() AB//ED
AB//ED
![]() CN//ED
CN//ED
![]()
![]()
![]()
![]()
![]() BF平分∠ABC, DF平分∠EDC,
BF平分∠ABC, DF平分∠EDC,
![]()
![]()
![]() FM//AB.
FM//AB.
![]()
![]() AB//ED
AB//ED
![]() FM//ED,
FM//ED,
![]()
![]()
即![]()
![]()
∠BFD与∠BCD的关系为:![]()


科目:初中数学 来源: 题型:
【题目】下列关系中,两个量之间为反比例函数关系的是( )
A.正方形的面积S与边长a的关系
B.正方形的周长L与边长a的关系
C.长方形的长为a,宽为20,其面积S与a的关系
D.长方形的面积为40,长为a,宽为b,a与b的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E、F分别为DC、BC边上的点,且∠EAF=45°,若将△ADE绕点A顺时针方向旋转90°得到△ABG.回答下列问题:
(1)∠GAF等于多少度?为什么?
(2)EF与FG相等吗?为什么?
(3)△AEF与△AGF有何种位置关系?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )

A.nB.2n-1C.![]() D.3(n+1)
D.3(n+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电动自动车已成为市民日常出行的首选工具.据某市某品牌电动自行车经销商1至3月份统计,该品牌电动自行车1月份销售150辆,3月份销售216辆.
(1)求该品牌电动自行车销售量的月均增长率;
(2)若该品牌电动自行车的进价为2300元,售价为2800元,则该经销商1至3月共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
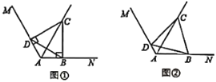
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于![]() 的二元一次方程组
的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)若上述方程组的解是等腰三角形的腰和底边的长,且这个等腰三角形周长为9,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
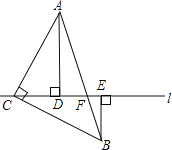
【题目】如图,将等腰直角三角形ABC的直角顶点置于直线![]() 上,且过A,B两点分别作直线l的垂线,垂足分别为D,E.
上,且过A,B两点分别作直线l的垂线,垂足分别为D,E.
(1)请你在图中找出一对全等三角形,并写出证明过程;
(2)若BE=3,DE=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有4张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长都是1,请在方格纸中分别画出符合要求的图形,所画图形各顶点必须与方格纸中小正方形的顶点重合,具体要求如下:
(1)画一个直角边长为4,面积为6的直角三角形.
(2)画一个底边长为4,面积为8的等腰三角形.
(3)画一个面积为5的等腰直角三角形.
(4)画一个边长为2![]() ,面积为6的等腰三角形.
,面积为6的等腰三角形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com