
【题目】小明家距离学校8千米,今天早晨,小明骑车上学图中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行驶的路程(千米)与他所用的时间(分钟)之间的关系.请根据图象,解答下列问题:

(1)小明行了多少千米时,自行车出现故障?修车用了几分钟?
(2)小明从早晨出发直到到达学校共用了多少分钟?
(3)小明修车前、后的行驶速度分别是多少?
(4)如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到或晚到多少分钟?
【答案】(1)小明行了3千米时,5(分钟);(2)30分钟到学校;(3)0.3(千米/分钟),![]() (千米/分钟);(4)他比实际情况早到
(千米/分钟);(4)他比实际情况早到![]() 分钟.
分钟.
【解析】
(1)根据自行车出现故障后路程s不变解答,修车的时间等于路程不变的时间;(2)路程等于8千米时的时间即为用的时间;(3)利用速度=路程÷时间分别列式计算即可得解;
(4)求出未出故障需用的时间,然后用实际情况的时间减去未出故障需用的时间即可得答案.
(1)由题图可知,小明行了3千米时,自行车出现故障,修车用了![]() (分钟).
(分钟).
(2)小明共用了30分钟到学校.
(3)修车前速度:![]() (千米/分钟),修车后速度:
(千米/分钟),修车后速度:![]() (千米/分钟).
(千米/分钟).
(4)![]() (分钟),
(分钟),![]() (分钟),
(分钟),
∴他比实际情况早到![]() 分钟.
分钟.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知:△ABC是等腰直角三角形,动点P在斜边AB所在的直线上,以PC为直角边作等腰直角三角形PCQ,其中∠PCQ=90°,探究并解决下列问题:
(1)如图①,若点P在线段AB上,且AC=1+ ![]() ,PA=
,PA= ![]() ,则:
,则:
① 线段PB= , PC= ;
② 猜想:PA2 , PB2 , PQ2三者之间的数量关系为;
(2)如图②,若点P在AB的延长线上,在(1)中所猜想的结论仍然成立,请你利用图②给出证明过程;
(3)若动点P满足 ![]() =
= ![]() ,求
,求 ![]() 的值.(提示:请利用备用图进行探求)
的值.(提示:请利用备用图进行探求)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABD和△ACD关于直线AD对称;在射线AD上取点E,连接BE, CE,如图:在射线AD上取点F连接BF, CF,如图,依此规律,第n个图形中全等三角形的对数是( )

A.nB.2n-1C.![]() D.3(n+1)
D.3(n+1)
查看答案和解析>>
科目:初中数学 来源: 题型:
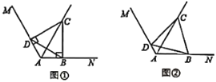
【题目】已知射线AC是∠MAN的角平分线, ∠NAC=60°, B, D分别是射线AN. AM上的点,连接BD.
(1)在图①中,若∠ABC=∠ADC=90°,求∠CDB的大小;
(2)在图②中,若∠ABC+∠ADC=180°,求证:四边形ABCD的面积是个定值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于![]() 的二元一次方程组
的二元一次方程组![]() 的解都为正数.
的解都为正数.
(1)求a的取值范围;
(2)若上述方程组的解是等腰三角形的腰和底边的长,且这个等腰三角形周长为9,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
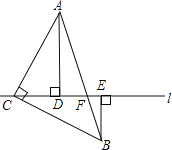
【题目】如图,将等腰直角三角形ABC的直角顶点置于直线![]() 上,且过A,B两点分别作直线l的垂线,垂足分别为D,E.
上,且过A,B两点分别作直线l的垂线,垂足分别为D,E.
(1)请你在图中找出一对全等三角形,并写出证明过程;
(2)若BE=3,DE=5,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某包装生产企业承接了一批礼品盒制作业务,为了确保质量,该企业进行试生产.他们购得规格是![]() 的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下
的标准板材作为原材料,每张标准板材再按照裁法一或裁法二裁下![]() 型与
型与![]() 型两种板材.如图所示,(单位:
型两种板材.如图所示,(单位:![]() )
)

(1)列出方程(组),求出图甲中![]() 与
与![]() 的值.
的值.
(2)在试生产阶段,若将![]() 张标准板材用裁法一裁剪,
张标准板材用裁法一裁剪,![]() 张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
张标准板材用裁法二裁剪,再将得到的A型与B型板材做侧面和底面,做成如图的竖式与横式两种无盖礼品盒.
①两种裁法共产生A型板材 张,B型板材 张;
②设做成的竖式无盖礼品盒![]() 个,横式无盖礼品盒的
个,横式无盖礼品盒的![]() 个,根据题意完成表格:
个,根据题意完成表格:
礼品盒板 材 | 竖式无盖(个) | 横式无盖(个) |
|
| |
A型(张) |
|
|
B型(张) |
|

③做成的竖式和横式两种无盖礼品盒总数最多是 个;
此时,横式无盖礼品盒可以做 个(在横线上直接写出答案,无需书写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的口袋里装有若干个相同的红球,为了用估计袋中红球的数量,八(1)班学生在数学实验室分组做摸球实验:每组先将10个与红球大小形状完全相同的白球装入袋中,搅匀后从中随机摸出一个球并记下颜色,再把它放回袋中,不断重复.下表是这次活动统计汇总各小组数据后获得的全班数据统计表:
摸球的次数s | 150 | 300 | 600 | 900 | 1200 | 1500 |
摸到白球的频数n | 63 | a | 247 | 365 | 484 | 606 |
摸到白球的频率 | 0.420 | 0.410 | 0.412 | 0.406 | 0.403 | b |
(1) 按表格数据格式,表中的![]() = ;
= ;![]() = ;
= ;
(2) 请估计:当次数s很大时,摸到白球的频率将会接近 (精确到0.1);
(3)请推算:摸到红球的概率是 (精确到0.1).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com