
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D、E,DF⊥AC于点F.
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的半径为10,sinB=![]() ,求阴影部分面积.
,求阴影部分面积.
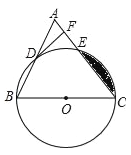
【答案】(1)证明见解析(2)DF与⊙O相切(3)![]()
【解析】
(1)连接CD,根据直径所对的圆周角为90°得∠BDC=90°,再由等腰三角形的三线合一得出结论;
(2)根据中位线的定义可以知道:OD是△ABC的中位线,则OD∥AC,因为DF⊥AC,所以DF⊥OD,得出DF与 O相切;
(3)如图3,连接OE、BE,先根据特殊的三角函数值求出∠ABC=60°,所以△ABC是等边三角形,求出直角△BEC各边的长,就可以求其面积,根据中线的性质可知△OEC的面积就是△BEC面积的-半,所求的阴影面积是扇形面积与△OEC的面积的差.
(1)连接CD
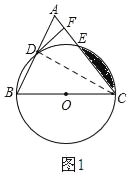
∵BC是⊙O的直径,
∴∠BDC=90°
又∵AC=BC,∴点D是AB的中点;
(2)DF与⊙O相切,
如图2,连接OD
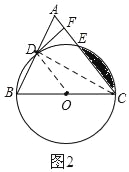
∵O是BC的中点,点D是AB的中点,
∴OD是△ABC的中位线,
∴OD∥AC
又∵DF⊥AC,
∴DF⊥OD,且OD是半径
∴DF与⊙O相切;
(3)如图3,连接OE,作OM⊥AC
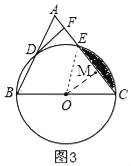
∵sin∠ABC=![]() ,
,
∴∠ABC=60°
又∵AC=BC,
∴△ABC是等边三角形
∴∠C=60°
又∵OE=OC
∴△OEC是等边三角形
∴EC=OC=10,∠EOC=60°
∵OM⊥AB,∠ACB=60°
∴MC=5,OM=![]() MC=5
MC=5![]()
∴S△OEC=![]() ×EC×OM=25
×EC×OM=25![]()
∴S阴影=S扇形OEC﹣S△OEC=![]() ﹣25
﹣25![]() =
=![]() ﹣25
﹣25![]()


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
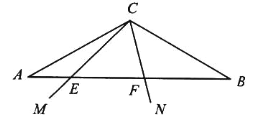
【题目】如图,在△ABC 中,∠A=∠B=30°,E,F 在 AB 上,∠ECF=60°.
(1)画出△BCF 绕点 C 顺时针旋转 120°后的△ACK;
(2)在(1)中,若 AE2+ EF2= BF2,求证 BF=![]() CF.
CF.
查看答案和解析>>
科目:初中数学 来源: 题型:
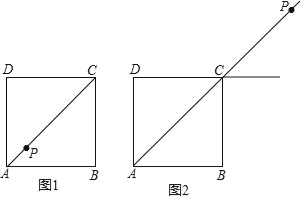
【题目】在正方形ABCD中,点P在射线AC上,作点P关于直线CD的对称点Q,作射线BQ交射线DC于点E,连接BP.
(1)当点P在线段AC上时,如图1.
①依题意补全图1;
②若EQ=BP,则∠PBE的度数为 ,并证明;
(2)当点P在线段AC的延长线上时,如图2.若EQ=BP,正方形ABCD的边长为1,请写出求BE长的思路.(可以不写出计算结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,⊙P的半径为1cm,且OP=6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么多少秒后⊙P与直线CD相切( )
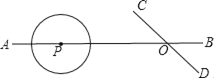
A. 4或8 B. 4或6 C. 8 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的中线,AE是BC边上的高.
(1)若∠ACB=100°,求∠CAE的度数;
(2)若S△ABC=12,CD=4,求高AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图.乙槽中有一圆柱形铁块放在其中(圆柱形铁块的下底面完全落在水槽底面上),现将甲槽中的水匀速注人乙槽.甲、乙两个水槽中水的深度![]() 与注水时间
与注水时间![]() (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
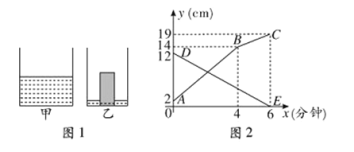
(1)图2中折线![]() 表示 槽中的水的深度与注水时间的关系,线段
表示 槽中的水的深度与注水时间的关系,线段![]() 表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点
表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点![]() 的纵坐标表示的实际意义是 ;
的纵坐标表示的实际意义是 ;
(2)当![]() 时,分别求出
时,分别求出![]() 和
和![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)注水多长时间时,甲、乙两个水槽中的水深度相同?
(4)若乙槽底面积为![]() 平方厘米(壁厚不计) ,求乙槽中铁块的体积.
平方厘米(壁厚不计) ,求乙槽中铁块的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
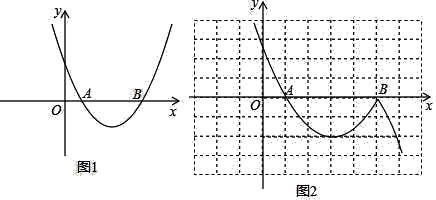
【题目】已知抛物线与x轴的交点坐标分别为A(1,0),B(x2,0)(点B在点A的右侧),其对称轴是x=3,该函数有最小值是﹣2.
(1)求二次函数解析式;
(2)在图1上作平行于x轴的直线,交抛物线于C(x3,y3),D(x4,y4),求x3+x4的值;
(3)将(1)中函数的部分图象(x>x2)向下翻折与原图象未翻折的部分组成图象“G”,如图2,在(2)中平行于x轴的直线取点E(x5,y5)、(x4<x5),结合函数图象求x3+x4+x5的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
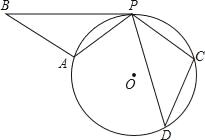
【题目】如图,已知△PDC是⊙O的内接三角形,CP=CD,若将△PCD绕点P顺时针旋转,当点C刚落在⊙O上的A处时,停止旋转,此时点D落在点B处.
(1)求证:PB与⊙O相切;
(2)当PD=2![]() ,∠DPC=30°时,求⊙O的半径长.
,∠DPC=30°时,求⊙O的半径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
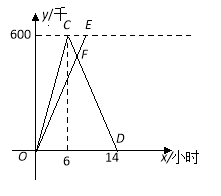
【题目】A,B两城相距600千米,甲、乙两车同时从A城出发驶向B城,甲车到达B城后立即返回.如图是它们离A城的距离y(千米)与行驶时间 x(小时)之间的函数图象.
(1)求甲车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(2)当它们行驶了7小时时,两车相遇,求乙车的速度及乙车行驶过程中y与x之间的函数解析式,并写出自变量x的取值范围;
(3)当两车相距100千米时,求甲车行驶的时间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com