
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,⊙P的半径为1cm,且OP=6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么多少秒后⊙P与直线CD相切( )
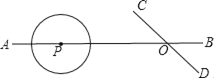
A. 4或8 B. 4或6 C. 8 D. 4
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,D在边AC上,且
,D在边AC上,且![]() .
.
![]() 如图1,填空
如图1,填空![]() ______
______![]() ,
,![]() ______
______![]()
![]() 如图2,若M为线段AC上的点,过M作直线
如图2,若M为线段AC上的点,过M作直线![]() 于H,分别交直线AB、BC与点N、E.
于H,分别交直线AB、BC与点N、E.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 试写出线段AN、CE、CD之间的数量关系,并加以证明.
试写出线段AN、CE、CD之间的数量关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
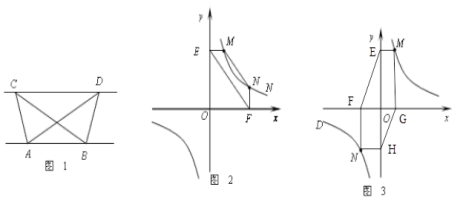
【题目】(1)探究新知:如图1,已知△ABC与△ABD的面积相等, 试判断AB与CD的位置关系,并说明理由.
(2)结论应用:如图2,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,垂足分别为E,F. 试证明:MN∥EF.
(3)变式探究:如图3,点M,N在反比例函数![]() (k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
(k>0)的图象上,过点M作ME⊥y轴,过点N作NF⊥x轴,过点M作MG⊥x轴,过点N作NH⊥y轴,垂足分别为E、F、G、H. 试证明:EF ∥GH.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程或方程组解应用题:
为了响应“十三五”规划中提出的绿色环保的倡议,某校文印室提出了每个人都践行“双面打印,节约用纸”.已知打印一份资料,如果用A4厚型纸单面打印,总质量为400克,将其全部改成双面打印,用纸将减少一半;如果用A4薄型纸双面打印,这份资料的总质量为160克,已知每页薄型纸比厚型纸轻0.8克,求A4薄型纸每页的质量.(墨的质量忽略不计)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】张大伯计划建一个面积为72平方米的矩形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙(墙长15米),另外的部分(包括中间的隔墙)用30米的竹篱笆围成,如图.
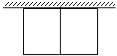
(1)请你通过计算帮助张大伯设计出围养鸡场的方案.
(2)在上述条件不变的情况下,能围出比72平方米更大的养鸡场吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)任意摸出1个球,记下颜色后不放回,再任意摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(2)现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
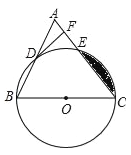
【题目】如图,已知在△ABC中,BC=AC,以BC为直径的⊙O与边AB、AC分别交于点D、E,DF⊥AC于点F.
(1)求证:点D是AB的中点;
(2)判断DF与⊙O的位置关系,并证明你的结论;
(3)若⊙O的半径为10,sinB=![]() ,求阴影部分面积.
,求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
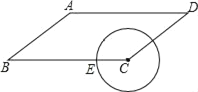
A. 0<CE≤8 B. 0<CE≤5 C. 3<CE≤8 D. 3<CE≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)勾股定理的证法多样,其中“面积法”是常用方法,小明发现:当四个全等的直角三角形如图摆放时,可以用“面积法”来证明勾股定理.(写出勾股定理的内容并证明)
(2)已知实数x,y,z满足:![]() ,试问长度分别为x、y、z的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
,试问长度分别为x、y、z的三条线段能否组成一个三角形?如果能,请求出该三角形的面积;如果不能,请说明理由.
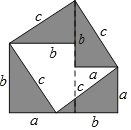
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com