
【题目】一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)任意摸出1个球,记下颜色后不放回,再任意摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(2)现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为![]() ,求n的值.
,求n的值.
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:
【题目】凯里市某文具店某种型号的计算器每只进价12元,售价20元,多买优惠,优势方法是:凡是一次买10只以上的,每多买一只,所买的全部计算器每只就降价0.1元,例如:某人买18只计算器,于是每只降价0.1×(18﹣10)=0.8(元),因此所买的18只计算器都按每只19.2元的价格购买,但是每只计算器的最低售价为16元.
(1)求一次至少购买多少只计算器,才能以最低价购买?
(2)求写出该文具店一次销售x(x>10)只时,所获利润y(元)与x(只)之间的函数关系式,并写出自变量x的取值范围;
(3)一天,甲顾客购买了46只,乙顾客购买了50只,店主发现卖46只赚的钱反而比卖50只赚的钱多,请你说明发生这一现象的原因;当10<x≤50时,为了获得最大利润,店家一次应卖多少只?这时的售价是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到新函数图象,其中原函数图象上的两点A(1,m)、B(4,n)平移后对应新函数图象上的点分别为点A′、B′.若阴影部分的面积为6,则新函数的表达式为( )
的图象沿y轴向上平移得到新函数图象,其中原函数图象上的两点A(1,m)、B(4,n)平移后对应新函数图象上的点分别为点A′、B′.若阴影部分的面积为6,则新函数的表达式为( )
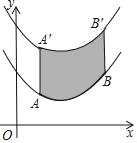
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学位为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计图表.
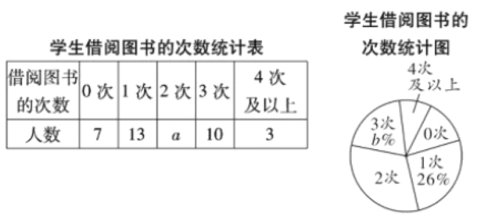
请你根据统计图表中的信息,解答下列问题:
(1)![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)该调查统计数据的中位数是_________,众数是__________;
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,⊙P的半径为1cm,且OP=6cm,如果⊙P以1cm/s的速度沿由A向B的方向移动,那么多少秒后⊙P与直线CD相切( )
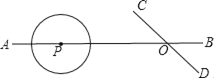
A. 4或8 B. 4或6 C. 8 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与抛物线C2互相依存.
(1)已知抛物线①:y=﹣2x2+4x+3与抛物线②:y=2x2+4x﹣1,请判断抛物线①与抛物线②是否互相依存,并说明理由.
(2)将抛物线C1:y=﹣2x2+4x+3沿x轴翻折,再向右平移m(m>0)个单位,得到抛物线C2,若抛物线C1与C2互相依存,求m的值.
(3)试问:如果对称轴不同的两条抛物线(二次函数图象)互相依存,那么它们的函数表达式中的二次项系数之间有什么数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图.乙槽中有一圆柱形铁块放在其中(圆柱形铁块的下底面完全落在水槽底面上),现将甲槽中的水匀速注人乙槽.甲、乙两个水槽中水的深度![]() 与注水时间
与注水时间![]() (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
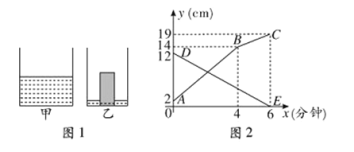
(1)图2中折线![]() 表示 槽中的水的深度与注水时间的关系,线段
表示 槽中的水的深度与注水时间的关系,线段![]() 表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点
表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点![]() 的纵坐标表示的实际意义是 ;
的纵坐标表示的实际意义是 ;
(2)当![]() 时,分别求出
时,分别求出![]() 和
和![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)注水多长时间时,甲、乙两个水槽中的水深度相同?
(4)若乙槽底面积为![]() 平方厘米(壁厚不计) ,求乙槽中铁块的体积.
平方厘米(壁厚不计) ,求乙槽中铁块的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
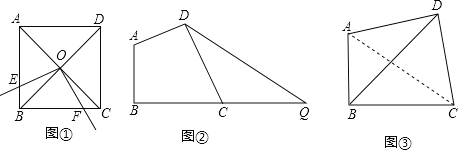
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
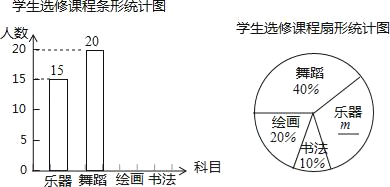
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com