
【题目】问题发现:
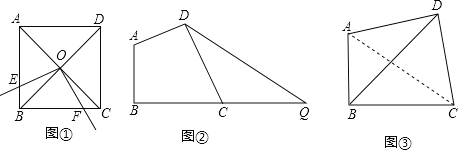
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
【答案】(1)4;(2)5![]() ;(3)600(
;(3)600(![]() +1).
+1).
【解析】
(1)如图①中,证明△EOB≌△FOC即可解决问题;
(2)如图②中,连接BD,取AC的中点O,连接OB,OD.利用四点共圆,证明∠DBQ=∠DAC=45°,再根据垂线段最短即可解决问题.
(3)如图③中,将△BDC绕点D顺时针旋转90°得到△EDA,首先证明AB+BC+BD=(![]() +1)BD,当BD最大时,AB+BC+BD的值最大.
+1)BD,当BD最大时,AB+BC+BD的值最大.
解:(1)如图①中,
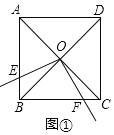
∵四边形ABCD是正方形,
∴OB=OC,∠OBE=∠OCF=45°,∠BOC=90°,
∵∠EOF=90°,
∴∠EOF=∠BOC,
∴∠EOB=∠FOC,
∴△EOB≌△FOC(SAS),
∴S△EOB=S△OFC,
∴S四边形OEBF=S△OBC=![]() S正方形ABCD=4,
S正方形ABCD=4,
故答案为:4;
(2)如图②中,连接BD,取AC的中点O,连接OB,OD.
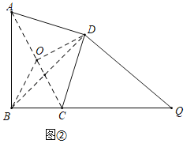
∵∠ABD=∠ADC=90°,AO=OC,
∴OA=OC=OB=OD,
∴A,B,C,D四点共圆,
∴∠DBC=∠DAC,
∵DA=DC,∠ADC=90°,
∴∠DAC=∠DCA=45°,
∴∠DBQ=45°,
根据垂线段最短可知,当QD⊥BD时,QD的值最短,DQ的最小值=![]() BQ=5
BQ=5![]() .
.
(3)如图③中,将△BDC绕点D顺时针旋转90°得到△EDA,
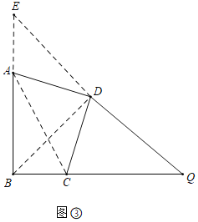
∵∠ABC+∠ADC=180°,
∴∠BCD+∠BAD=∠EAD+BAD=180°,
∴B,A,E三点共线,
∵DE=DB,∠EDB=90°,
∴BE=![]() BD,
BD,
∴AB+BC=AB+AE=BE=![]() BD,
BD,
∴BC+BC+BD=(![]() +1)BD,
+1)BD,
∴当BD最大时,AB+BC+BD的值最大,
∵A,B,C,D四点共圆,
∴当BD为直径时,BD的值最大,
∵∠ADC=90°,
∴AC是直径,
∴BD=AC时,AB+BC+BD的值最大,最大值=600(![]() +1).
+1).


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
【题目】已知k为实数,关于x的方程为x2﹣2(k+1)x+k2=0.
(1)请判断x=﹣1是否可为此方程的根,说明理由.
(2)设方程的两实根为x1,x2,当2x1+2x2+1=x1x2时,试求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋中装有4个只有颜色不同的球,其中1个黄球、1个蓝球、2个红球.
(1)任意摸出1个球,记下颜色后不放回,再任意摸出1个球.求两次摸出的球恰好都是红球的概率(要求画树状图或列表);
(2)现再将n个黄球放入布袋,搅匀后,使任意摸出1个球是黄球的概率为![]() ,求n的值.
,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
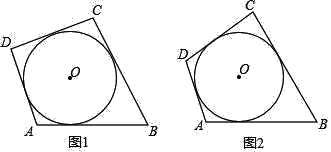
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平行四边形ABCD中,AB=5,BC=8,cosB=![]() ,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
,点E是BC边上的动点,当以CE为半径的⊙C与边AD有两个交点时,半径CE的取值范围是( )
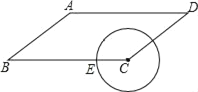
A. 0<CE≤8 B. 0<CE≤5 C. 3<CE≤8 D. 3<CE≤5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
科目:初中数学 来源: 题型:
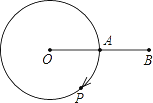
【题目】如图,A是半径为6cm的⊙O上的定点,动点P从A出发,以πcm/s的速度沿圆周按顺时针方向运动,当点P回到A时立即停止运动.设点P运动时间为t(s);
(1)当t=6s时,∠POA的度数是________;
(2)当t为多少时,∠POA=120°;
(3)如果点B是OA延长线上的一点,且AB=AO,问t为多少时,△POB为直角三角形?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
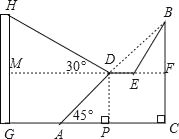
【题目】为邓小平诞辰110周年献礼,广安市政府对城市建设进行了整改,如图,已知斜坡AB长60![]() 米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
米,坡角(即∠BAC)为45°,BC⊥AC,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线CA的休闲平台DE和一条新的斜坡BE(下面两个小题结果都保留根号).
(1)若修建的斜坡BE的坡比为![]() :1,求休闲平台DE的长是多少米?
:1,求休闲平台DE的长是多少米?
(2)一座建筑物GH距离A点33米远(即AG=33米),小亮在D点测得建筑物顶部H的仰角(即∠HDM)为30°.点B、C、A、G,H在同一个平面内,点C、A、G在同一条直线上,且HG⊥CG,问建筑物GH高为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校团委举办了一次“中国梦我的梦”演讲比赛满分10分,学生得分均为整数,成绩达6分以上(含6分)为合格,达到9分以上(含9分)为优秀.如图所示是这次竞赛中甲、乙两组学生成绩分布的条形统计图.
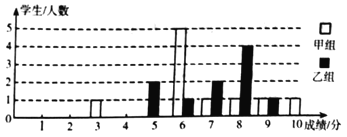
(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲 | 6 | 3.41 | 90% | 20% | |
乙 | 7.1 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是______组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com