
【题目】(类比概念)三角形的内切圆是以三个内角的平分线的交点为圆心,以这点到三边的距离为半径的圆,则三角形可以称为圆的外切三角形,可以得出三角形的三边与该圆相切.以此类推,如图1,各边都和圆相切的四边形称为圆外切四边形
(性质探究)如图1,试探究圆外切四边形的ABCD两组对边AB,CD与BC,AD之间的数量关系
猜想结论: (要求用文字语言叙述)
写出证明过程(利用图1,写出已知、求证、证明)
(性质应用)
①初中学过的下列四边形中哪些是圆外切四边形 (填序号)
A:平行四边形:B:菱形:C:矩形;D:正方形
②如图2,圆外切四边形ABCD,且AB=12,CD=8,则四边形的周长是 .
③圆外切四边形的周长为48cm,相邻的三条边的比为5:4:7,求四边形各边的长.
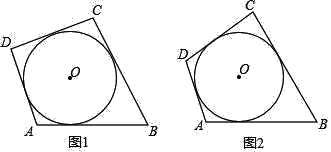
【答案】见解析.
【解析】
(1)根据切线长定理即可得出结论;
(2)①圆外切四边形是内心到四边的距离相等,即可得出结论;
②根据圆外切四边形的对边和相等,即可求出结论;
③根据圆外切四边形的性质求出第四边,利用周长建立方程求解即可得出结论.
性质探讨:圆外切四边形的对边和相等,理由:
如图1,已知:四边形ABCD的四边AB,BC,CD,DA都于⊙O相切于G,F,E,H.
求证:AD+BC=AB+CD.
证明:∵AB,AD和⊙O相切,∴AG=AH,同理:BG=BF,CE=CF,DE=DH,∴AD+BC=AH+DH+BF+CF=AG+BG+CE+DE=AB+CD,即:圆外切四边形的对边和相等.
故答案为:圆外切四边形的对边和相等;
性质应用:①∵根据圆外切四边形的定义得:圆心到四边的距离相等.
∵平行四边形和矩形不存在一点到四边的距离相等,而菱形和正方形对角线的交点到四边的距离相等.
故答案为:B,D;
②∵圆外切四边形ABCD,∴AB+CD=AD+BC.
∵AB=12,CD=8,∴AD+BC=12+8=20,∴四边形的周长是AB+CD+AD+BC=20+20=40.
故答案为:40;
③∵相邻的三条边的比为5:4:7,∴设此三边为5x,4x,7x,根据圆外切四边形的性质得:第四边为5x+7x﹣4x=8x.
∵圆外切四边形的周长为48cm,∴4x+5x+7x+8x=24x=48,∴x=2,∴此四边形的四边为4x=8cm,5x=10cm,7x=14cm,8x=16cm.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】学校开展“书香校园”活动以来,受到同学们的广泛关注,学位为了解全校学生课外阅读的情况,随机调查了部分学生在一周内借阅图书的次数,并制成如下不完整的统计图表.
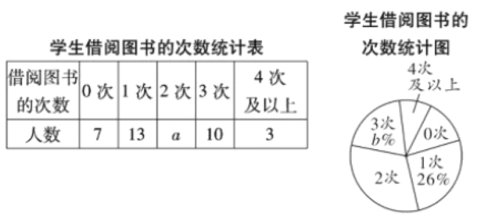
请你根据统计图表中的信息,解答下列问题:
(1)![]() =___________,
=___________,![]() =_____________;
=_____________;
(2)该调查统计数据的中位数是_________,众数是__________;
(3)请计算扇形统计图中“3次”所对应扇形的圆心角的度数;
(4)若该校共有2000名学生,根据调查结果,估计该校学生在一周内借阅图书“4次及以上”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与抛物线C2互相依存.
(1)已知抛物线①:y=﹣2x2+4x+3与抛物线②:y=2x2+4x﹣1,请判断抛物线①与抛物线②是否互相依存,并说明理由.
(2)将抛物线C1:y=﹣2x2+4x+3沿x轴翻折,再向右平移m(m>0)个单位,得到抛物线C2,若抛物线C1与C2互相依存,求m的值.
(3)试问:如果对称轴不同的两条抛物线(二次函数图象)互相依存,那么它们的函数表达式中的二次项系数之间有什么数量关系?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是甲、乙两个圆柱形水槽的轴截面示意图.乙槽中有一圆柱形铁块放在其中(圆柱形铁块的下底面完全落在水槽底面上),现将甲槽中的水匀速注人乙槽.甲、乙两个水槽中水的深度![]() 与注水时间
与注水时间![]() (分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
(分钟)之间的关系如图2所示.根据图象提供的信息,解答下列问题:
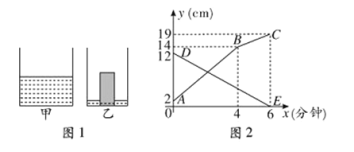
(1)图2中折线![]() 表示 槽中的水的深度与注水时间的关系,线段
表示 槽中的水的深度与注水时间的关系,线段![]() 表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点
表示 槽中的水的深度与注水时间的关系(填“甲”或“乙”),点![]() 的纵坐标表示的实际意义是 ;
的纵坐标表示的实际意义是 ;
(2)当![]() 时,分别求出
时,分别求出![]() 和
和![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(3)注水多长时间时,甲、乙两个水槽中的水深度相同?
(4)若乙槽底面积为![]() 平方厘米(壁厚不计) ,求乙槽中铁块的体积.
平方厘米(壁厚不计) ,求乙槽中铁块的体积.
查看答案和解析>>
科目:初中数学 来源: 题型:
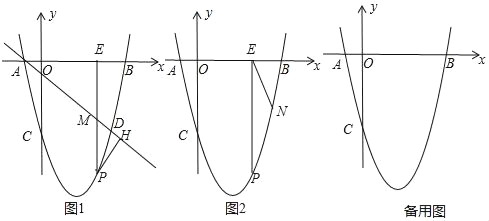
【题目】如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点A的坐标为(﹣1,0),且OC=OB,tan∠OAC=4.
(1)求抛物线的解析式;
(2)若点D和点C关于抛物线的对称轴对称,直线AD下方的抛物线上有一点P,过点P作PH⊥AD于点H,作PM平行于y轴交直线AD于点M,交x轴于点E,求△PHM的周长的最大值.
(3)在(2)的条件下,如图2,在直线EP的右侧、x轴下方的抛物线上是否存在点N,过点N作NG⊥x轴交x轴于点G,使得以点E、N、G为顶点的三角形与△AOC相似?如果存在,请直接写出点G的坐标:如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题发现:
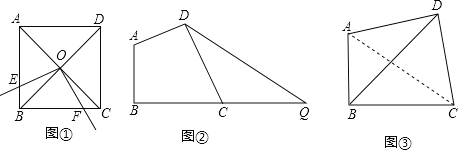
(1)如图①,正方形ABCD的边长为4,对角线AC、BD相交于点O,E是AB上点(点E不与A、B重合),将射线OE绕点O逆时针旋转90°,所得射线与BC交于点F,则四边形OEBF的面积为 .
问题探究:
(2)如图②,线段BQ=10,C为BQ上点,在BQ上方作四边形ABCD,使∠ABC=∠ADC=90°,且AD=CD,连接DQ,求DQ的最小值;
问题解决:
(3)“绿水青山就是金山银山”,某市在生态治理活动中新建了一处南山植物园,图③为南山植物园花卉展示区的部分平面示意图,在四边形ABCD中,∠ABC=∠ADC=90°,AD=CD,AC=600米.其中AB、BD、BC为观赏小路,设计人员考虑到为分散人流和便观赏,提出三条小路的长度和要取得最大,试求AB+BD+BC的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小美周末去公园玩,发现公园一角有一种“守株待兔”的游戏,该游戏老板说明游戏规则如下:提供一只兔子和一个有A、B、C、D、E五个出口的兔笼,而且笼内的兔子从每个出口走出兔笼的机会是均等的,玩家只能将兔子从A、B两个出入口放兔子,如果兔子进笼子后从开始进入的入口出来,则玩家可获得价值5元的小兔玩具一只,否则,应付3元的参与费用.
(1)用作表或树状图列出小美参与游戏的所有可能结果,并求出小美得到玩具兔子的概率.
(2)假设有100人玩这个游戏,估计老板约赚多少钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2011山东济南,27,9分)如图,矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线![]() 经过A、C两点,与AB边交于点D.
经过A、C两点,与AB边交于点D.
(1)求抛物线的函数表达式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式,并求出m为何值时,S取得最大值;
②当S最大时,在抛物线![]() 的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
的对称轴l上若存在点F,使△FDQ为直角三角形,请直接写出所有符合条件的F的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com